

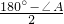 =
=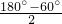 =60°,
=60°,

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大七年级版 2009-2010学年 第16期 总第172期 华师大版 题型:044
阅读下列材料,回答问题:
材料:探照灯、蜗行天线、汽车灯以及很多灯具都与抛物线形状有关,如图(1)是一探照灯的灯碗,从侧面上看,从位于E点的灯泡发出的两束光线EA、EC经灯碗反射后平行射出,如果图中的∠BAE=α,∠DCE=β,则∠AEC的度数应怎样表示?
问题1:请求出材料中的∠AEC的度数.
问题2:爱动脑筋的小杰同学想:在图(1)中的这三个角有这样的特定关系,那么当点E在图(2)-(4)这些位置时,且AB∥CD,∠BAE、∠DCE和∠AEC之间有什么关系呢?你能帮小杰同学解决这个问题吗?请写出这三幅图中的规律,并选取其中的一个给予证明.
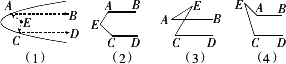
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com