
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
【答案】C
【解析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,由PE+PM=PE′+PM=E′M知点P、M即为使PE+PM取得最小值的点,利用S菱形ABCD=![]() ACBD=ABE′M求得E′M的长即可得答案.
ACBD=ABE′M求得E′M的长即可得答案.
如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,

则点P、M即为使PE+PM取得最小值的点,
则有PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵AC=6![]() ,BD=6,
,BD=6,
∴AB=![]() ,
,
由S菱形ABCD=![]() ACBD=ABE′M得
ACBD=ABE′M得![]() ×6
×6![]() ×6=3
×6=3![]() E′M,
E′M,
解得:E′M=2![]() ,
,
即PE+PM的最小值是2![]() ,
,
故选C.


科目:初中数学 来源: 题型:
【题目】小马虎解方理![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
(1)小马虎解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF. 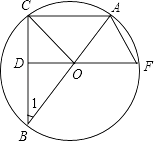
(1)求证:△COD≌△BOD;
(2)填空:①当∠1=时,四边形OCAF是菱形; ②当∠1=时,AB=2 ![]() OD.
OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, ![]() =2.236)
=2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
我们知道,当a>0且b>0时,( ![]() ﹣
﹣ ![]() )2≥0,所以a﹣2
)2≥0,所以a﹣2 ![]() +≥0,从而a+b≥2
+≥0,从而a+b≥2 ![]() (当a=b时取等号),
(当a=b时取等号),
【获得结论】设函数y=x+ ![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= ![]() 即x=
即x= ![]() 时,函数y有最小值为2
时,函数y有最小值为2 ![]()
(1)【直接应用】
若y1=x(x>0)与y2= ![]() (x>0),则当x=时,y1+y2取得最小值为 .
(x>0),则当x=时,y1+y2取得最小值为 .
(2)【变形应用】
若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则 ![]() 的最小值是
的最小值是
(3)【探索应用】
在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= ![]() 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S
①求S与x之间的函数关系式;
②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.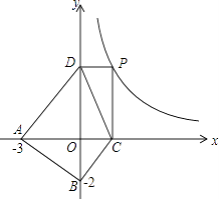
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照如下步骤计算:6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ).
).
(1)计算:( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )的结果.
)的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com