
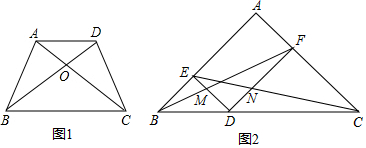
分析 (1)在梯形ABCD中,AD∥BC,根据同底等高的三角形的面积相等得到S△ABC=S△DCB,根据面积的和差即可得到结论;
(2)连接MN,根据相似三角形的性质得到$\frac{FN}{DN}$=$\frac{FC}{ED}$,$\frac{FM}{BM}$=$\frac{FD}{BE}$,推出MN∥BC,根据等腰三角形的判定即可得到结论.
解答  证明:(1)∵在梯形ABCD中,AD∥BC,
证明:(1)∵在梯形ABCD中,AD∥BC,
∴S△ABC=S△DCB,
∵S△ABC-S△BOC=S△DCB-S△BOC,
∴S△AOB=S△DOC;
(2)连接MN,
∵DE∥AC,
∴△EDN∽△CFN,
∴$\frac{FN}{DN}$=$\frac{FC}{ED}$,
同理$\frac{FM}{BM}$=$\frac{FD}{BE}$,
∵AB=AC,∠A=90°,
∴∠ABC=∠ACB=45°,∵DE∥AC,DF∥AB,
∴∠BED=∠CFD=90°,∠BDE=∠CDF=45°,
∴FC=FD,ED=BE,∴$\frac{FC}{ED}$=$\frac{FD}{BE}$,
∴$\frac{FN}{DN}$=$\frac{FM}{BM}$,
∴MN∥BC,
∴∠NMD=∠BDE=45°,∠MND=∠CDF=45°,
∴∠NMD=∠MND,
∴DM=DN.
点评 本题考查了梯形,相似三角形的判定和性质,平行线的判定和性质,知道同底等高的三角形的面积相等是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
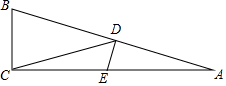 如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.
如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
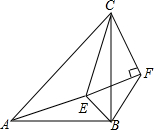 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
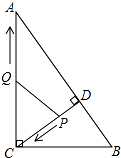 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.
在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
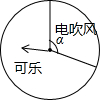 为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 72 | 142 | 278 | 355 | b | 701 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.72 | 0.71 | 0.695 | a | 0.705 | 0.701 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com