
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
【答案】解:(1)设生产A种产品x件,则生产B种产品(10﹣x)件,于是有
x+3(10﹣x)=14,
解得:x=8,
则10﹣x=10﹣8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)设应生产A种产品x件,则生产B种产品有(10﹣x)件,由题意有:![]() ,
,
解得:2≤x<8;
所以可以采用的方案有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种方案;
,共6种方案;
(3)设总利润为y万元,生产A种产品x件,则生产B种产品(10﹣x)件,
则利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
所以当![]() 时可获得最大利润,其最大利润为2×1+8×3=26万元.
时可获得最大利润,其最大利润为2×1+8×3=26万元.
【解析】(1)设生产A种产品x件,则生产B种产品有(10﹣x)件,根据计划获利14万元,即两种产品共获利14万元,即可列方程求解;
(2)根据计划投入资金不多于44万元,且获利多于14万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数;
(3)得出利润y与A产品数量x的函数关系式,根据增减性可得,B产品生产越多,获利越大,因而B取最大值时,获利最大,据此即可求解.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F;
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
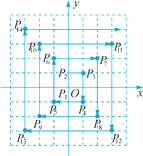
【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:点P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),….根据这个规律,求点P2018的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
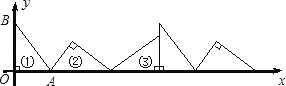
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com