
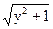 )(y+
)(y+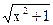 )=1.求证:x+y=0.
)=1.求证:x+y=0.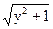 )(y+
)(y+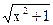 )=
)=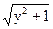 (y+1)>1,与已知矛盾.
(y+1)>1,与已知矛盾.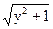 )(y+
)(y+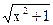 )=
)= 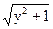 (y+1)<
(y+1)< 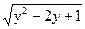 (1+y)=(1-y)(1+y)=1-y2<1,
(1+y)=(1-y)(1+y)=1-y2<1,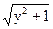 )(y+
)(y+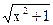 )>1,与已知矛盾.
)>1,与已知矛盾.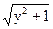 )(y+
)(y+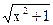 )=
)=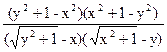
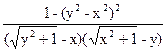 ≤
≤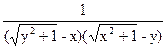
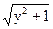 -x>1,
-x>1,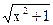 -y>1,则
-y>1,则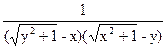 <1,
<1,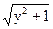 )(y+
)(y+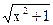 )>(
)>( 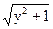 -y)(
-y)( 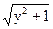 +y)=1,与已知矛盾.
+y)=1,与已知矛盾.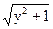 )(y+
)(y+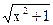 )<(
)<(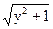 -y)(
-y)( 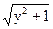 +y)=1,
+y)=1,

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com