
分析 (1)根据题意可以写出y与x的函数关系式,从而可以解答本题;
(2)根据题意可以得到关于x的不等式,再根据(1)中的函数解析式可以解答本题.
解答 解:(1)由题意可得,
y=1200x+2000(20-x)=-800x+40000,
即y与x之间的函数关系式是y=-800x+40000;
(2)由题意可得,
x$≥\frac{2}{3}(20-x)$,
解得,x≥8,
∵y=-800x+40000,
∴当x=8时,y取得最大值,此时y=33600,
答:运往省城直接批发给零售商8吨,在本地市场零售12吨,才能使张华所获纯利润最大,最大纯利润是33600元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的思想和不等式的性质解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
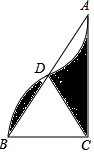 如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为4$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com