
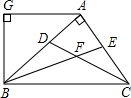
 如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )
如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )| A. | ①③ | B. | ②④ | C. | ①③④ | D. | ①②③④ |
分析 根据平行线的性质、角平分线的定义进行计算,判断即可,
解答 解:∵AG∥BC,
∴∠BAG=∠ABC,
∵BE是∠ABC的角平分线,
∴∠ABC=2∠ABF,
∴∠BAG=2∠ABF,①正确;
BA不一定平分∠CBG,②错误;
∵AB⊥AC,AG⊥BG,
∴∠BAG+∠ABG=90°,∠ABC+∠ACB=90°,
∵AG∥BC,
∴∠BAG=∠ABC,
∴∠ABG=∠ACB,③正确;
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
∵CD、BE分别是∠ACD,∠ABC的角平分线,
∴∠FBC+∠FCB=45°,
∴∠CFB=135°,④正确,
故选:C.
点评 本题考查的是角平分线的定义、平行线的性质、三角形内角和定理的应用,掌握相关的判定定理和性质定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
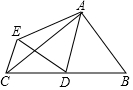 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )
先阅读材料再回答问题:如图线段AB=4,AC=1,BD=2,且AC⊥AB,BD⊥AB,点P在线段AB上运动,当AP=a时,则BP=4-a,PC=$\sqrt{1{+a}^{2}}$,PD=$\sqrt{4{+(4-a)}^{2}}$,由此可求得CP+DP的最小值为5.那么请问:代数式$\sqrt{4{+x}^{2}}$+$\sqrt{16{+(5-x)}^{2}}$的最小值为( )| A. | 10 | B. | 2$\sqrt{10}$ | C. | $\sqrt{61}$ | D. | $\sqrt{41}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com