
【题目】问题背景:
图1,等腰△ABC中,AB=AC,∠BAC=120°,过点A作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°;于是
∠BAC=60°;于是![]() =
=![]() =
=![]() ;
;

(1)迁移应用:
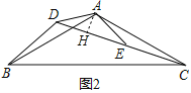
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.求证:CD=![]() AD+BD;
AD+BD;
(2)拓展延伸
如图图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.若AE=5,CE=2,求BF的长.
【答案】(1)见解析;(2)BF=3![]() .
.
【解析】
(1)作AH⊥CD于H,易证△DAB≌△EAC,得BD=CE,由∠ADH=30°,得DH=![]() AD,结合DH=HE,即可得到结论;
AD,结合DH=HE,即可得到结论;
(2)作BH⊥AE于H,连接BE,易得BC=BE=BD=BA,从而得A、D、E、C四点共圆,进而得△EFC是等边三角形,可得FH=4.5,结合∠BFH=30°,即可求解.
(1)如图2中,作AH⊥CD于H.
∵△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,
∴AD=AE,AB=AC,∠DAB=∠EAC,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∵∠ADH=(180°-120°)÷2=30°,
∴在Rt△ADH中,DH=![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=![]() AD+BD;
AD+BD;
(2)如图3中,作BH⊥AE于H,连接BE.
∵四边形ABCD是菱形,∠ABC=120°,
∴△ABD,△BDC是等边三角形,
∴BA=BD=BC,
∵E、C关于BM对称,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四点共圆,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等边三角形,
∴EC=EF=2,
∵AE=5,
∴AH=HE=2.5,
∴FH=4.5,
∵在Rt△BHF中,∠BFH=30°,
∴![]() =cos30°,
=cos30°,
∴BF=4.5÷![]() =3
=3![]() .
.


科目:初中数学 来源: 题型:
【题目】先化简,再求值:![]() ,其中|x|≤1,且x为整数.
,其中|x|≤1,且x为整数.
小海同学的解法如下:
解:原式=![]() ﹣
﹣![]() ①
①
=(x﹣1)2﹣x2+3 ②
=x2﹣2x﹣1﹣x2+3 ③
=﹣2x+2.④
当x=﹣1时,⑤
原式=﹣2×(﹣1)+2⑥
=2+2=4.⑦
请指出他解答过程中的错误(写出相应的序号,多写不给分),并写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,在△ABE中,∠AEB=90°,AE与BC交于点F.
(1)若∠BAE=30°,BF=2![]() ,求BE的长;
,求BE的长;
(2)如图2,D为BE延长线上一点,连接AD、FD、CD,若AB=AD,∠ACD=135°,求证:BD+BF=AF.
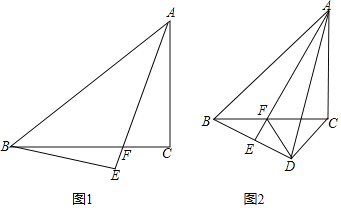
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,ABCD为矩形,以CD为直径作半圆,矩形的另外三边分别与半圆相切,沿着折痕DF折叠该矩形,使得点C的对应点E落在AB边上,若AD=2,则图中阴影部分的面积为_____.
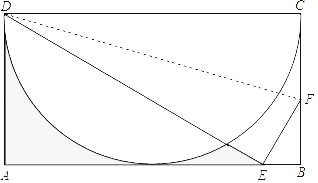
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线形拱桥,正常水位桥下面宽度为![]() 米,拱顶距离水平面
米,拱顶距离水平面![]() 米,如图建立直角坐标系,若正常水位时,桥下水深
米,如图建立直角坐标系,若正常水位时,桥下水深![]() 米,为保证过往船只顺利航行,桥下水面宽度不得小于
米,为保证过往船只顺利航行,桥下水面宽度不得小于![]() 米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
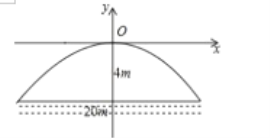
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的汉字书写能力,某学校连续举办了几届汉字听写大赛,今年经过层层选拔,确定了参加决赛的选手,决赛的比赛规则是每正确听写出1个汉字得2分,满分是100分,下面是根据决赛的成绩绘制出的不完整的频数分布表、扇形统计图和频数分布直方图.
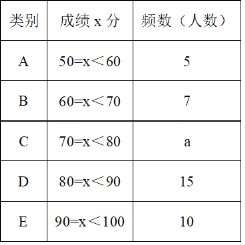
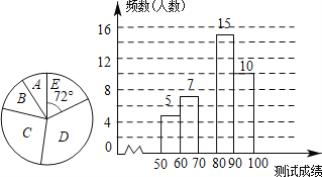
请结合图表完成下列各题
(1)表中a的值为______,并把频数分布直方图补充完整;
(2)学校想利用频数分布表估计这次决赛的平均成绩,请你直接写出平均成绩;
(3)通过与去年的决赛成绩进行比较,发现今年各类人数的中位数有了显著提高,提高了15%以上,求去年各类人数的中位数最高可能是多少?
(4)想从A类学生的3名女生和2名男生中选出两人进行培训,直接写出选中1名男生和1名女生的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com