
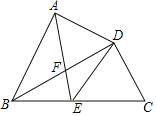
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F,若BC=4,∠CBD=30°,则AE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
如图,作EH⊥AB于H,利用∠CBD的余弦可求出BD的长,利用∠ABD的余弦可求出AB的长,利用∠EBH的正弦和余弦可求出BH、HE的长,即可求出AH的长,利用勾股定理求出AE的长即可.
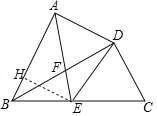
如图,作EH⊥AB于H,
在Rt△BDC中,BC=4,∠CBD=30°,
∴BD=BC·cos30°=2![]() ,
,
∵BD平分∠ABC,∠CBD=30°,
∴∠ABD=30°,∠EBH=60°,
在Rt△ABD中,∠ABD=30°,BD=2![]() ,
,
∴AB=BD·cos30°=3,
∵点E为BC中点,
∴BE=EC=2,
在Rt△BEH中,BH=BE·cos∠EBH=1,HE=EH·sin∠EBH=![]() ,
,
∴AH=AB-BH=2,
在Rt△AEH中,AE=![]() =
=![]() ,
,
故选:D.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.其中,1和0既不是质数也不是合数.数学家欧几里得在《几何原本》中对此进行过详细论述.一个较大自然数是质数还是合数通常用“N法”来判断,主要分为三个步骤:第一步,找出大于N且最接近N的平方数![]() ;第二步,用小于
;第二步,用小于![]() 的所有质数去除N;第三步,如果这些质数都不能整除N,那么N就是质数;如果这些质数中至少有一个能整除N,那么N就是合数.如判断239是质数还是合数?第一步,
的所有质数去除N;第三步,如果这些质数都不能整除N,那么N就是质数;如果这些质数中至少有一个能整除N,那么N就是合数.如判断239是质数还是合数?第一步,![]() ;第二步,小于 16的质数有: 2、3、5、7、11、13,用2、3、5、7、11、13 依次去除239;第三步,发现没有质数能整除239,所以239是质数.
;第二步,小于 16的质数有: 2、3、5、7、11、13,用2、3、5、7、11、13 依次去除239;第三步,发现没有质数能整除239,所以239是质数.
分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(a, b, c…是不相等的质数,m,n,p… 是正整数),则合数N共有
…(a, b, c…是不相等的质数,m,n,p… 是正整数),则合数N共有![]() …个约数.如
…个约数.如![]() ,
, ![]() ,则8共有4 个约数;又如
,则8共有4 个约数;又如![]() ,则12共有6个约数.
,则12共有6个约数.
请用以上方法解决下列问题:
(1)请用“ N法”判断619是质数还是合数?
(2)求有18个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
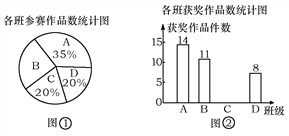
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
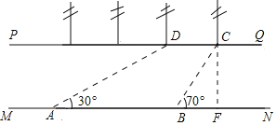
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③abc>0;④b2+8a>4ac.其中正确的有( )
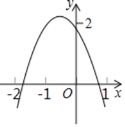
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是
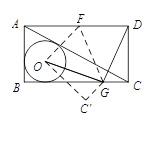
A.CD+DF=4B.CDDF=2![]() 3
3
C.BC+AB=2![]() +4D.BCAB=2
+4D.BCAB=2
查看答案和解析>>
科目:初中数学 来源: 题型:
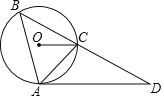
【题目】如图,在△ABC中,∠ABC=45°,它的外接圆的圆心O在其内部,连结OC,过点A作AD∥OC,交BC的延长线于点D.
(1)求证:AD是⊙O的切线;
(2)若∠BAD=105°,⊙O的半径为2,求劣弧AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com