
【题目】已知抛物线交x轴于A,B两点(A在B右边),A(3,0),B(1,0)交y轴于C点,C(0,3),连接AC;
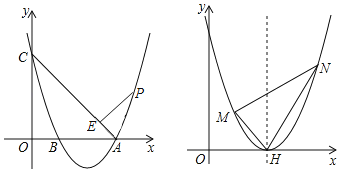
(1)求抛物线的解析式;
(2)P为抛物线上的一点,作PE⊥CA于E点,且CE=3PE,求P点坐标;
(3)将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,过H作直线MH,NH,当MH⊥NH时,求MN恒过的定点坐标.
【答案】(1)y=x2﹣4x+3;(2)(2,﹣1)或(![]() ,
,![]() );(3)MN恒过的定点(2,1)
);(3)MN恒过的定点(2,1)
【解析】
(1)用待定系数解答便可;
(2)分两种情况:P点AC的上方,点P在AC的下方.过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,与PD交于点G,证明EF=3EG,设EG=m,用m的代数式表示P点的横纵坐标,再代入二次函数解析式,便可求得m的值,进而得P点的坐标;
(3)过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,先求出H点的坐标与新抛物线的解析式,设出M、N的坐标,得出两坐标的联系,表示出MN的解析式,再代入定点(2,1)的坐标进行验证便可得解.
(1)∵抛物线过A(3,0),B(1,0),
∴可设抛物线的解析式为y=a(x﹣3)(x﹣1)(a≠0),
把c(0,3)代入,得3a=3,
∴a=1,
∴抛物线的解析式是y=(x﹣3)(x﹣1)=x2﹣4x+3,
即y=x2﹣4x+3;
(2)当P点在AC上方时,过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,如图1,

∵A(3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=45°,
∵FG∥OA,
∴∠CEF=45°,
∴CF=EF=![]() CE,
CE,
∵PE⊥CA,
∴∠PEG=45°,
∴PG=EG=![]() PE,
PE,
∵CE=3PE,
∴EF=3FG,
设EF=3m,则PG=EG=m,FG=4m,
∴DG=OF=OC﹣CF=3﹣3m,
PD=PG+DG=3﹣2m,
∴P(4m,3﹣2m),
把P(4m,3﹣2m)代入y=x2﹣4x+3中得,
3﹣2m=16m2﹣16m+3,
∴m=![]() ,或m=0(舍去),
,或m=0(舍去),
∴P(![]() ,
,![]() );
);
当P点AC下方时,如图2,过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,
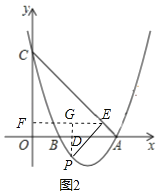
∵A(3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=45°,
∵FE∥OA,
∴∠CEF=45°,
∴CF=EF=![]() CE,
CE,
∵PE⊥CA,
∴∠PEG=45°,
∴PG=EG=![]() PE,
PE,
∵CE=3PE,
∴EF=3FG,
设EF=3m,则PG=EG=m,EG=2m,
∴DG=OF=OC﹣CF=3﹣3m,
PD=PG﹣DG=4m﹣3,
∴P(2m,3﹣4m),
把P(2m,3﹣4m)代入y=x2﹣4x+3中得,
3﹣4m=4m2﹣8m+3,
∴m=1,或m=0(舍去),
∴P(2,﹣1);
综上,P点的坐标为(2,﹣1)或(![]() ,
,![]() );
);
(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线y=x2﹣4x+3的顶点为(2,﹣1),
∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,
∴H(2,0),
由题意知,点H是新抛物线的顶点,
∴新抛物线的解析式为y=(x﹣2)2,
设M(m,(m﹣2)2),N(n,(n﹣2)2),
过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,如图3,

则MK=(m﹣2)2,KH=2﹣m,HL=n﹣2,NL=(n﹣2)2,
∵MH⊥NH,
∴∠MHK+∠HMK=∠MHK+∠NHL=90°,
∴∠HMK=∠NHL,
∵∠MKH=∠HLN=90°,
∴△KHM∽△LNH,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
设直线MN的解析式为:y=kx+b(k≠0),则 ,
,
∴ ,
,
∴直线MN的解析式为:![]() ,
,
当x=2时,![]() =(m-2)2﹣(m2﹣4m+3)
=(m-2)2﹣(m2﹣4m+3)
=m2﹣4m+4﹣m2+4m﹣3=1,
∴MN恒过的定点(2,1).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线.以
的角平分线.以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,设![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
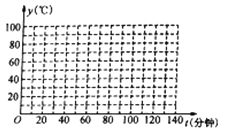
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
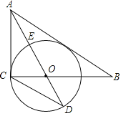
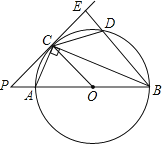
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下的统计图,请你结合图中所给的信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是 ;
(3)若该校七年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
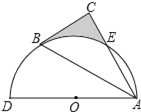
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() .
.
(1)求证:不论![]() 为何实数,该抛物线与
为何实数,该抛物线与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)若抛物线的对称轴为直线![]() ,求
,求![]() 的值和
的值和![]() 点坐标;
点坐标;
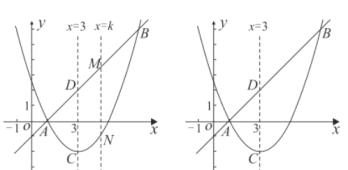
(3)如图,直线![]() 与(2)中的抛物线并于
与(2)中的抛物线并于![]() 两点,并与它的对称轴交于点
两点,并与它的对称轴交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .求当
.求当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形.
为顶点的四边形为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,若反比例函数
,若反比例函数![]() 的图象恰好经过
的图象恰好经过![]() 的中点
的中点![]() ,则
,则![]() 的值是( )
的值是( )

A.24B.25C.26D.30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com