
| A. | 392 | B. | 402 | C. | 412 | D. | 422 |
分析 根据选项的数值,得到ab+1的值,进一步根据平方差公式得到ab的乘积形式,再根据质数的定义即可求解.
解答 解:A、当ab+1=392时,ab=392-1=40×38,与a,b为两质数且相差2不符合,故本选项错误;
B、当ab+1=402时,ab=402-1=41×39,与a,b为两质数且相差2不符合,故本选项错误;
C、当ab+1=412时,ab=412-1=42×40,与a,b为两质数且相差2不符合,故本选项错误;
D、当ab+1=422时,ab=422-1=43×41,正好与a,b为两质数且相差2符合,故本选项正确,
故选:D.
点评 本题考查的是因式分解的应用,质数的定义,解答此类题目的关键是得到ab是哪两个相差为2的数的积.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形的边长均为1的方格纸中有线段AC和EF,点A、C、E、F均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中有线段AC和EF,点A、C、E、F均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
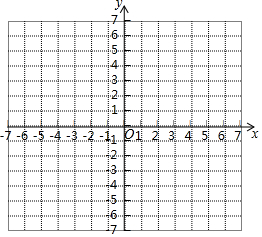 在如图所示平面直角坐标系中,已知A(-2,2),B(-3,-2),C(3,-2).
在如图所示平面直角坐标系中,已知A(-2,2),B(-3,-2),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
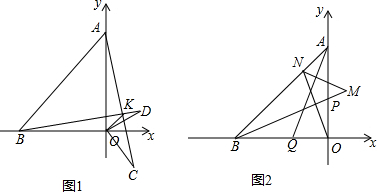
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com