
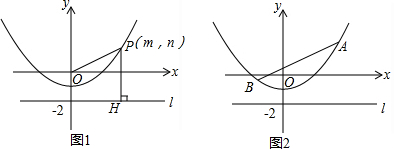
分析 (1)m=0时,直接代入x=0,得P(0,-1),则OP,PH长易知.当m=4时,直接代入x=4,得P(4,3),OP可有勾股定理求得,PH=yP-(-2).
(2)猜想OP=PH.证明时因为P为所有满足二次函数y=$\frac{{x}^{2}}{4}$-1的点,一般可设(m,$\frac{{m}^{2}}{4}$-1).类似(1)利用勾股定理和PH=yP-(-2)可求出OP与PH,比较即得结论.
(3)考虑(2)结论,即函数y=$\frac{{x}^{2}}{4}$-1的点到原点的距离等于其到l的距离.要求A、B两点到l距离的和,即A、B两点到原点的和,若AB不过点O,则OA+OB>AB=8,若AB过点O,则OA+OB=AB=8,所以OA+OB≥8,即A、B两点到l距离的和≥8,进而最小值即为8.
解答 解:(1)解:如图1,
记PH与x轴交点为Q,
当m=0时,P(0,-1).此时OP=1,PH=1.
当m=4时,P(4,3).此时PQ=3,OQ=4,
∴OP=$\sqrt{P{Q}^{2}+O{Q}^{2}}$=5,PH=yP-(-2)=3-(-2)=5.
故答案为:1,1;5,5;
(2)猜想:OP=PH.
证明:如图2,
∵P在二次函数y=$\frac{{x}^{2}}{4}$-1上,
∴设P(m,$\frac{{m}^{2}}{4}$-1),则PQ=|$\frac{{m}^{2}}{4}$-1|,OQ=|m|,
∵△OPQ为直角三角形,
∴OP=$\sqrt{P{Q}^{2}+O{Q}^{2}}$=$\sqrt{(\frac{{m}^{2}}{4}-1)^{2}+{m}^{2}}$=$\frac{{m}^{2}}{4}$+1
PH=yp-(-2)=$(\frac{{m}^{2}}{4}-1)-(-2)=\frac{{m}^{2}}{4}+1$
∴OP=PH.
(3)解:如图2,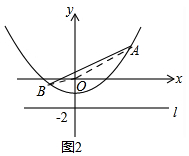
连接OA,OB,
过点A作AC⊥l于C,过点B作BD⊥l于D,
此时AC即为A点到l的距离,
BD即为B点到l的距离.
①当AB不过O点时,连接OA,OB,
在△OAB中,OA+OB>AB=8,
由上述结论得:AC=OA,BD=OB,
∴AC+BD>8,
②当AB过O点时,AC+BD=OA+OB=AB=8,所以AC+BD的最小值为8,
即A,B两点到直线l的距离之和的最小值为8.
点评 此题是二次函数综合题,主要考查了学生对函数与其图象的理解,另外涉及一些点到直线距离,利用勾股定理就坐标系中两点间的距离及最短距离等知识点,总体来说难度不高,但知识新颖易引发学生对数学知识的兴趣,非常值得学生练习.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -4 | -1 | 0 | 1 | … |
| y | … | -2 | 1 | -2 | -7 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x+6与x轴、y轴交于A、B两点,直线l经过原点,与线段AB交于点C.
如图,直线y=2x+6与x轴、y轴交于A、B两点,直线l经过原点,与线段AB交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 △ABC和△FED中,AD=FC,∠A=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).
△ABC和△FED中,AD=FC,∠A=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 不等边三角形 | D. | 直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com