练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    实数， ， ， ， 中，其中无理数出现的频数是______________．

    【解析】根据题意可知无理数有： 和π，因此其出现的频数为2. 故答案为：2.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新疆阿克苏十二中2017-2018学年八年级（上）期中数学试卷 题型：单选题

    如图，在△ABC中，∠A＝80°，∠B＝40°，D，E分别是AB，AC上的点，且DE∥BC，则∠AED的度数为（　　）

    A. 40° B. 60° C. 80° D. 120°

    B 【解析】试题分析：本题考查了三角形内角和定理、平行线的性质．解题时，要挖掘出隐含在题干中的已知条件：三角形的内角和是180°.根据两直线平行（DE∥BC），同位角相等（∠ADE=∠B）可以求得△ADE的内角∠ADE=40°；然后在△ADE中利用三角形内角和定理即可求得∠AED的度数．∵DE∥BC（已知），∠B=40°（已知），∴∠ADE=∠B=40°（两直线平行，同位角相等）；又∵∠A=...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省鞍山市铁西区2017-2018学年七年级（上）期中数学试卷 题型：填空题

    列式表示：x的一半与y的2倍的差为__________________.

    【解析】试题分析：被减数为：x的一半；减数为：y的2倍；求差即可． 【解析】 x的一半为：x，y的2倍为2y．它们的差为：x﹣2y．

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：解答题

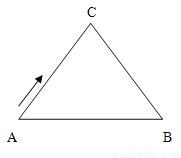
    如图，△ABC中，AC＝BC＝10 cm，AB＝12 cm，点D是AB的中点，连结CD，动点P从点A出发，沿A→C→B的路径运动，到达点B时运动停止，速度为每秒2 cm，设运动时间为秒．

    （1）求CD的长；

    （2）当为何值时，△ADP是直角三角形？

    （3）直接写出：当为何值时，△ADP是等腰三角形？

    （1）8；（2）1.8；（3）1.8或5；（3）当或或或时，△ADP是等腰三角形． 【解析】试题分析：（1）根据题意，运用等腰三角形的性质，求得AD的长，再根据勾股定理求得CD的长即可； （2）分两种情况进行讨论：当DP⊥AC时，△ADP是直角三角形，当PD⊥AD时，△ADP是直角三角形，分别根据相似三角形的性质求解即可； （3）分三种情况进行讨论：当PA=PD时，当AP=AD时...

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：解答题

    计算：

    -1． 【解析】试题分析：根据乘方的意义、算术平方根、立方根计算即可. 试题解析：【解析】 原式=1－5＝

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：单选题

    已知等腰三角形的顶角为50°，则这个等腰三角形的底角为（ ）

    A．50° B．65° C．80° D．50°或65°

    B 【解析】 试题分析：根据等腰三角形的性质及三角形内角和定理进行解答即可． 【解析】 ∵等腰三角形的顶角为50°， ∴这个等腰三角形的底角==65°． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型：解答题

    已知抛物线的图象与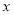轴有两个公共点．

    （1）求的取值范围，写出当取其范围内最大整数时抛物线的解析式；

    （2）将（1）中所求得的抛物线记为，

    ①求的顶点的坐标；

    ②若当时， 的取值范围是，求的值；

    （3）将平移得到抛物线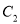,使的顶点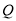落在以原点为圆心半径为的圆上，求点与两点间的距离最大时的解析式，怎样平移可以得到所求抛物线？

    （1）;(2) ①,②1；（3）的解析式为．将抛物线记为向左平移,再向上平移即可得到抛物线． 【解析】试题分析：（1）函数图形与x轴有两个公共点，则该函数为二次函数且△＞0，故此可得到关于m的不等式组，从而可求得m的取值范围； （2）①把（1）中求得的函数解析式改为顶点式，即可得出顶点P的坐标； ②先求得抛物线的对称轴，当1≤x≤n时，函数图象位于对称轴的右侧，y随x的增大而增大...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型：单选题

    已知二次函数的图象与轴的一个交点为（1,0），则它与轴的另一个交点坐标是（ ）

    A. （1，0） B. （2，0） C. （－2，0） D. （－1，0）

    C 【解析】试题分析：把x＝1，y＝0代入y＝x2＋bx－2得： 0＝1＋b－2， ∴b＝1， ∴对称轴为x＝＝， ∴x＝＝， ∴x2＝－2， 它与x轴的另一个交点坐标是（－2，0）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年八年级（上）期中数学模拟试卷 题型：填空题

    如图：已知∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF若“SAS”为依据，还要添加的条件为_____．

    BC=EF或BE=CF 【解析】如图，若要以“SAS”为依据，证明△ABC≌△DEF， ∵∠ABC=∠DEF，AB=DE， ∴只需对应角∠ABC和∠DEF的另一边相等即可， ∴BC=EF或BE=CF， 故答案为：BC=EF或BE=CF．

    查看答案和解析>>

    同步练习册答案