
| 3x2+2x |
| x2+x+0.25 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3x2+x+2 |
| x2+2x+1 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
| 3x2+2x |
| x2+x+0.25 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3x2+x+2 |
| x2+2x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料:求函数![]() 的最大值.
的最大值.
解:将原函数转化成![]() 的一元二次方程,得
的一元二次方程,得![]() .
.
∵![]() 为实数,∴△=
为实数,∴△=![]() =
=![]() 0.
0.
∴![]() .因此,
.因此,![]() 的最大值为4.
的最大值为4.
根据材料给你的启示,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源:2013年江苏省无锡市中考数学模拟试卷(一)(解析版) 题型:解答题
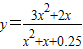 的最大值.
的最大值.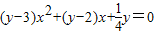 .
.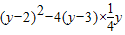 =-y+4≥0,∴y≤4.因此,y的最大值为4.
=-y+4≥0,∴y≤4.因此,y的最大值为4.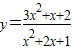 的最小值.
的最小值.查看答案和解析>>
科目:初中数学 来源:2013年广东省中考数学模拟试卷(五)(解析版) 题型:解答题
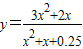 的最大值.
的最大值.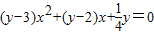 .
.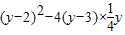 =-y+4≥0,∴y≤4.因此,y的最大值为4.
=-y+4≥0,∴y≤4.因此,y的最大值为4. 的最小值.
的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com