

���� ��1�����������ε����ʼ����жϣ�
��2����������1���еĽ�����Ȼ������ֻҪ֤����DAF�ա�BAE�������Ƴ�DF=BE����ADF=��ABR���ɡ�AFD=��BFH�������Ƴ���DAF=��BHF=90�㣻
��3����ͼ3�У�����BD�����ɹ��ɶ����ɵ�BD=$\sqrt{2}$����֤��DE=DB���ɽ�����⣻
��4����ͼ4�У���M��N��G��H�ֱ���BD��DE��EF��BF���е㣬����BE��DF��MN��NG��GH��HM��EB��DF��O��MN��DF��P��������������λ�߶���������֤���ı���MNGH�����Σ���֤����NMH=90�㼴�ɽ�����⣮
��� �⣺��1����ͼ1�У�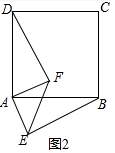
���ı���ABCD�������Σ�
���DAB=90�㣬AD=AB��
��AF=AE��
��BE=DF��BE��DF��
�ʴ�ΪBE=DF��BE��DF
��2����1���еĽ�����Ȼ������
���ɣ���ͼ2�У��ӳ�DF��BE��H��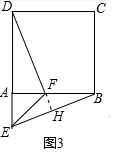
���ı���ABCD�������Σ�
��AD=AB��AF=AE����DAB=��FAE=90�㣬
�ڡ�DAF�͡�BAE�У�
$\left\{\begin{array}{l}{DA=BA}\\{��DAF=��BAE}\\{AF=AE}\end{array}\right.$��
���DAF�ա�BAE��
��DF=BE����ADF=��ABR��
�ߡ�AFD=��BFH��
���DAF=��BHF=90�㣬
��DF��BE��
��3����ͼ3�У�����BD��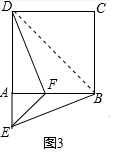
��Rt��ABD����AD=AB=1��
��BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
��DF��ֱƽ���߶�EB��
��DE=DB=$\sqrt{2}$��
��AE=DE-AD=$\sqrt{2}$-1��
�ʴ�Ϊ$\sqrt{2}$-1��
��4����ͼ4�У���M��N��G��H�ֱ���BD��DE��EF��BF���е㣬����BE��DF��MN��NG��GH��HM��EB��DF��O��MN��DF��P��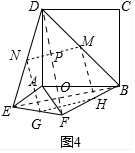
��֤��DF=EB��DF��EB��
��DN=NE��DM=MB��
��MN��EB��MN=$\frac{1}{2}$EB��ͬ����֤GH��EB��GH=$\frac{1}{2}$EB��MH��DF��MH=$\frac{1}{2}$DF��GN��DF��GN=$\frac{1}{2}$DF��
��MN=NG=GH=HM��
���ı���MNGH�����Σ�
��MN��EB��
���DPM=��DOB=90�㣬
��DF��MH��
���NMH=��DPM=90�㣬
���ı���MNGH�������Σ�
�ʴ�Ϊ������
���� ���⿼���ı����ۺ��⡢�����ε����ʡ�ȫ�������ε��ж������ʡ������ε���λ�߶������߶δ�ֱƽ���ߵ����ʡ����ɶ�����֪ʶ������Ĺؼ�����ȷѰ��ȫ�������ν�����⣬ѧ�����ӳ��ø����ߣ������п�ѹ���⣮


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com