
分析 (1)根据抛物线的解析式求出A、B的坐标,进而得到AB的长;
(2)先求出点C的坐标,再以AB为底,OC为高求出△ABC的面积;
(3)先求出顶点P的坐标,设抛物线的对称轴与x轴交于点M,再根据S四边形ABPC=S△AOC+S梯形OCPM+S△BMP,计算即可求解.
解答 解:(1)∵y=2x2-4x-1,
∴令y=0,得2x2-4x-1=0,
求得A($\frac{2-\sqrt{6}}{2}$,0),B($\frac{2+\sqrt{6}}{2}$,0),
∴AB=$\frac{2+\sqrt{6}}{2}$-$\frac{2-\sqrt{6}}{2}$=$\sqrt{6}$;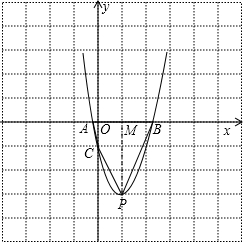 (2)∵y=2x2-4x-1,
(2)∵y=2x2-4x-1,
∴令x=0,得C(0,-1),
∴S△ABC=$\frac{1}{2}$×$\sqrt{6}$×1=$\frac{\sqrt{6}}{2}$;
(3)∵y=2x2-4x-1=2(x-1)2-3,
∴顶点P(1,-3).
设抛物线的对称轴与x轴交于点M,则M(1,0).
S四边形ABPC=S△AOC+S梯形OCPM+S△BMP
=$\frac{1}{2}$×$\frac{\sqrt{6}-2}{2}$×1+$\frac{1}{2}$×(1+3)×1+$\frac{1}{2}$×3×($\frac{2+\sqrt{6}}{2}$-1)
=$\frac{\sqrt{6}-2}{4}$+2+$\frac{3\sqrt{6}}{4}$
=$\sqrt{6}$+$\frac{3}{2}$.
点评 本题考查了抛物线与x轴的交点以及二次函数的性质,得出各点的坐标是解答本题的突破口,另外注意将不规则图形的面积转化为几个规则图形的面积和进行求解.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:解答题
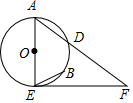 如图,AE为⊙O的直径,D为$\widehat{AB}$的中点,过E点的切线交AD的延长线于F.
如图,AE为⊙O的直径,D为$\widehat{AB}$的中点,过E点的切线交AD的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
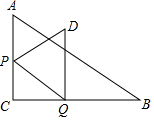 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
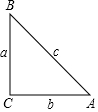 如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.
如图,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,tanA=$\frac{a}{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
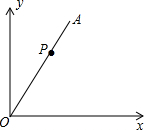 如图,已知P是∠AOC的边OA上一点,且点A的坐标为(3,4),则sin∠AOC的值是( )
如图,已知P是∠AOC的边OA上一点,且点A的坐标为(3,4),则sin∠AOC的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com