解:(1)这个显然是一个分段函数,
y=20-
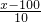
×0.8
=-0.08x+28,(100≤x<200)
可见x=200元时,y=28-16=12(万件)
y=12-
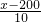
×1=-0.1x+32,(200≤x≤300).
(2)投资成本为480+1520=2000万元
y=-0.08x+28,100≤x<200,
w=xy-40y-2000
=(x-40)(-0.08x+28)-2000
=-0.08x
2+31.2x-3120
=-0.08(x-195)
2-78
可见第一年在100≤x<200注定亏损,x=195时亏损最少,为78万元
200≤x≤300,y=-0.1x+32,
w=xy-40y-2000
=(x-40)(-0.1x+32)-2000
=-0.1x
2+36x-3280
=-0.1(x-180)
2-40
可见第一年在200≤x≤300注定亏损,x=200时亏损最少,为80万元
综上可见,x=195时亏损最少,为78万元.
(3)根据第二年的盈利为1840万元,第二年:100≤x≤200时,
第二年盈利=xy-40y=-0.08(x-195)
2+1922=1840,
整理得出:0.08(x-195)
2=82,
(x-195)
2=1025,
x-195=±5

,
∴x
1=195+5

≈195+5×6.40=227(不合题意舍去);
x
2=195-5

≈195-5×6.40=163元.
答:第二年此情况下该产品销售单价为163元时,第二年的盈利为1840万元.
分析:(1)分段讨论当100<x≤200和当200<x≤300的函数关系式,
(2)由年获利=年销售额-生产成本-节电投资分别列出当100<x≤200和200<x≤300的利润关系式,求出最大利润,
(3)依题意可知,当100<x≤200时,写出第二年w与x关系为式,由第二年的盈利为1840万元,解得单价x.
点评:本题主要考查了二次函数在实际中应用,最大销售利润的问题常利函数的增减性来解答,我们首先要弄懂题意,确定变量,建立函数模型解答,其中要注意应该在自变量的取值范围内求最大值.

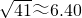 ,
,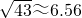 )
)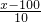 ×0.8
×0.8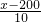 ×1=-0.1x+32,(200≤x≤300).
×1=-0.1x+32,(200≤x≤300). ,
, ≈195+5×6.40=227(不合题意舍去);
≈195+5×6.40=227(不合题意舍去); ≈195-5×6.40=163元.
≈195-5×6.40=163元.

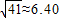 ,
,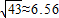 )
)