
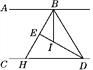
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
【答案】(1)详见解析;(2)∠EBI=![]() ∠BHD,理由详见解析.
∠BHD,理由详见解析.
【解析】试题分析:(1)根据角平分线的定义可得∠ABD=2∠EBD,∠BDC=2∠BDE,然后求出∠ABD+∠BDC=180°,再根据同旁内角互补,两直线平行证明;
(2)由AB∥CD,得到∠ABH=∠BHD,再由BI平分∠EBD,BH平分∠ABD,即可得出结论.
试题解析:
(1)证明:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠BDC=2∠BDE,
∵∠EBD+∠EDB=90°,
∴∠ABD+∠BDC=2×90°=180°,
∴AB∥CD;
(2)∠EBI=![]() ∠BHD. 理由如下:
∠BHD. 理由如下:
因为AB∥CD,
所以∠ABH=∠BHD.
因为BI平分∠EBD,BH平分∠ABD,
所以∠EBI=![]() ∠EBD=
∠EBD=![]() ∠ABH=
∠ABH=![]() ∠BHD.
∠BHD.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
一般地,n个相同的因数a相乘![]() 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式 。
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:anam=an+m以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G。
DC,连接EF并延长交BC的延长线于点G。
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G。
DC,连接EF并延长交BC的延长线于点G。
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45![]() ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com