
分析 (1)根据平均单价=$\frac{两次购买粮食的总金额}{两次购买粮食的重量和}$,代入可得结论;
(2)先计算张飞两次购买的粮食重量,再代入平均单价=$\frac{两次购买粮食的总金额}{两次购买粮食的重量和}$,计算即可;
(3)利用差比较大小,小的合算.
解答 解:(1)孔明第一次购买粮食付款100x元,第二次购买粮食付款100y元,两次共付款(100x+100y)元.
∵平均单价=$\frac{两次购买粮食的总金额}{两次购买粮食的重量和}$,
∴Q1=$\frac{100x+100y}{100+100}$=$\frac{x+y}{2}$;
(2)张飞第一次购买粮食$\frac{100}{x}$千克,第二次购买粮食$\frac{100}{y}$千克,故两次共购买粮食$(\frac{100}{x}+\frac{100}{y})$千克,
∵平均单价=$\frac{两次购买粮食的总金额}{两次购买粮食的重量和}$,
∴Q2=$\frac{100+100}{\frac{100}{X}+\frac{100}{Y}}$=$\frac{2xy}{x+y}$;
(3)要判断谁更合算,就是判断Q1、Q2的大小,小的更合算些,
∵Q1-Q2=$\frac{x+y}{2}$-$\frac{2xy}{x+y}$=$\frac{(x-y)^{2}}{2(x+y)}$,且x≠y,
∴(x-y)2>0而2(x+y)>0,
∴Q1-Q2>0,
故Q1>Q2,
∴张飞的购粮方式更合算.
点评 本题考查了分式的混合运用和实际应用问题,明确平均单价=$\frac{两次购买粮食的总金额}{两次购买粮食的重量和}$是本题的关键,同时要注意分式大小的比较,方法较多,本题利用了作差比较大小,另外还可以作商、平方法等比较大小.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
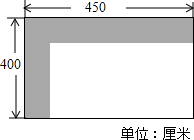 小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米,那么小路的宽度应为0.5米.
小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米,那么小路的宽度应为0.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com