
【题目】在![]() 中,
中,![]() ,把
,把![]() 绕AB边上的点D顺时针旋转
绕AB边上的点D顺时针旋转![]() 得到
得到![]() 交AB于点E,若
交AB于点E,若![]() ,则
,则![]() 的面积是
的面积是![]()
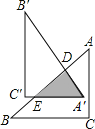
A. 3 B. 5 C. 11 D. 6
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,∠COE=140°,将一直角三角板AOB的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
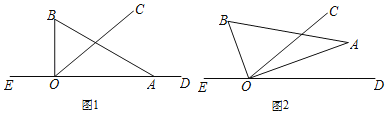
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,求此时∠BOC的度数;
(2)若射线OC的位置保持不变,在旋转过程中,是否存在某个时刻,使得射线OA、OC、OD中的某一条射线是另两条射线所成夹角的角平分线?若存在,请求出t的取值,若不存在,请说明理由;
(3)若在三角板开始转动的同时,射线OC也绕O点以每秒15°的速度逆时针旋转一周,从旋转开始多长时间,射线OC平分∠BOD.直接写出t的值.(本题中的角均为大于0°且小于180°的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以A为圆心适当长为半径画弧,分别交AC、AB于点M、N,分别以点M、N为圆心,大于![]() MN的长为半径画弧交于点P,作射线AP交BC于点D,再作射线DE交AB于点E,则下列结论错误的是( )
MN的长为半径画弧交于点P,作射线AP交BC于点D,再作射线DE交AB于点E,则下列结论错误的是( )
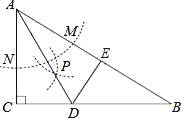
A. ∠ADB=120° B. S△ADC:S△ABC=1:3
C. 若CD=2,则BD=4 D. DE垂直平分AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
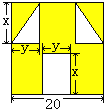
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
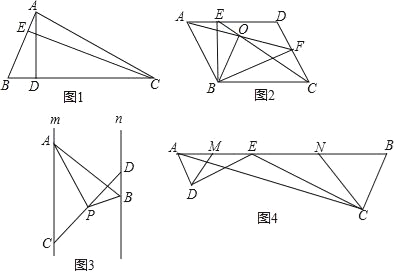
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
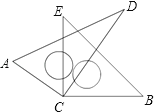
【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=25°,求∠ACB的度数.
(2)若∠ACB=140°,求∠DCE的度数.
(3)猜想∠ACB与∠DCE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题.
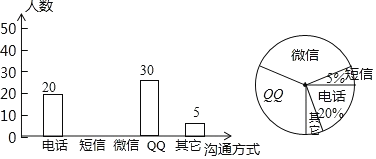
(1)这次统计共抽查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校共有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com