Question

如图，AB∥CD，直线a交AB、CD分别于点E、F，点M在线段EF上（点M不与E、F重合），P是直线CD上的一个动点（点P不与F重合），∠AEF=n⁰，求∠FMP+∠FPM的度数．

Answer 1

∠FMP+∠FPM=180°﹣n°．

试题分析：由于点P的位置不能确定，故应分点P在F的左侧与右侧两种情况进行讨论，当点P在F的左侧时，由AB∥CD，利用两直线平行，同旁内角互补，可得∠AEF十∠EFC=180°，又由三角形内角和定理，即可得∠FMP+∠FPM+∠EFC=180°，则可得∠FMP+∠FPM=∠AEF；点P在F的右侧时，由AB∥CD，利用两直线平行，内错角相等，即可证得∠AEF=∠EFD，又由三角形内角和定理，即可得∠FMP+∠FPM+∠EFD=180°，则可得∠FMP+∠FPM+∠AEF=180°．
试题解析：当点P在F的左侧时，如图1所示，
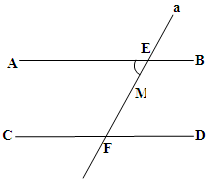
∵AB∥CD，
∴∠AEF十∠EFC=180°，
∵∠FMP+∠FPM+∠EFC=180°，
∴∠FMP+∠FPM=∠AEF，即∠FMP+∠FPM=n°；
当点P在F的右侧时，如图2所示，
∵AB∥CD，
∴∠AEF=∠EFD，
∵∠FMP+∠FPM+∠EFD=180°，
∴∠FMP+∠FPM+∠AEF=180°，即∠FMP+∠FPM=180°﹣n°．
．
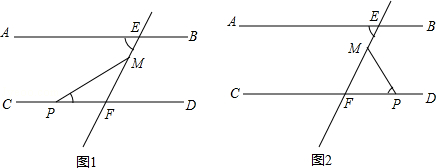
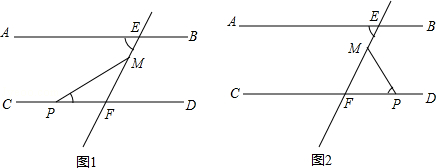