
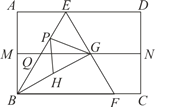
【题目】如图,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,把纸片
,把纸片![]() 对折,折痕为
对折,折痕为![]() ,展开后再过点
,展开后再过点![]() 折叠该纸片,使点
折叠该纸片,使点![]() 落在
落在![]() 上的点
上的点![]() 处,且折痕
处,且折痕![]() 与
与![]() 相交于点
相交于点![]() ,再次展平后,连接
,再次展平后,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() ,
,![]() 的长;
的长;
(3)![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是 .(请直接写出结果)
的最小值是 .(请直接写出结果)
【答案】(1)详见解析;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)连接AG,根据垂直平分线的性质和折叠的性质得出AG=AB=BG,由此得出△ABG为等边三角形,根据等边三角形的性质和三角形内角和定理即可得出△EBF为等边三角形.
(2)设AE=x,则BE=2x,根据勾股定理可求出AE的长度,则BE的长度可求,根据![]() 是等边三角形求出BF的长度,利用三角形中位线即可求出QG的长度;
是等边三角形求出BF的长度,利用三角形中位线即可求出QG的长度;
(3)根据题意可得出M点与H点关于BE所在直线对称,所以P与Q重合时,PH+PG的值最小,最小值为MG的长度,进而问题可解.
(1)如图,连接AG
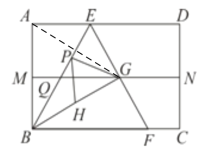
∵MN垂直平分AB
∴AG=BG
根据轴对称的性质,可得
AB=BG,
∴AG=AB=BG.
∴△ABG为等边三角形.
![]()
∴∠ABE=30°,∠AEB=∠GEB=60°
又∵∠EBF=60°
![]()
∴△EBF为等边三角形
(2)由(1)得∠ABE=30°
设AE=x,则BE=2x
∵AB=2,![]()
∴![]()
即![]() ,
,![]()
∵△EBF为等边三角形
![]()
∴![]()
(3)根据条件易知M点与H点关于BE所在直线对称
∴P与Q重合时,PH+PG的值最小
又∵![]() ,
,![]()
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
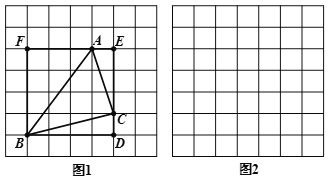
【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
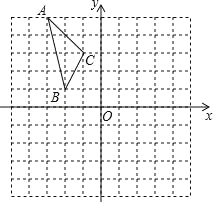
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和![]() 关于原点O成中心对称图形,画出图形并写出
关于原点O成中心对称图形,画出图形并写出![]() 的各顶点的坐标;
的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到![]() ,画出图形,求出线段AC扫过部分的面积.
,画出图形,求出线段AC扫过部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
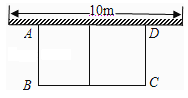
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,解一元一次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”思想求方程![]() =x的解.
=x的解.
(3)如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边沿BA、AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
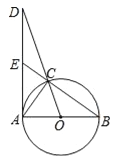
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
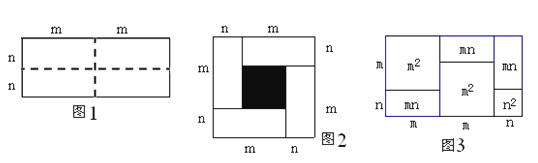
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com