
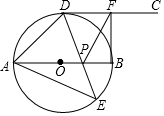
 如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.
如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.分析 (1)要证明CD∥AB,只要证明∠ODF=∠AOD即可,根据题目中的条件可以证明∠ODF=∠AOD,从而可以解答本题;
(2)①根据四边形ADFP是菱形和菱形的性质,可以求得∠DAE的度数;
②根据四边形BFDP是正方形,可以求得∠DAE的度数.
解答  (1)证明:连接OD,如右图所示,
(1)证明:连接OD,如右图所示,
∵射线DC切⊙O于点D,
∴OD⊥CD,
即∠ODF=90°,
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
∴∠ODF=∠AOD,
∴CD∥AB;
(2)①连接AF与DP交于点G,如右上图所示,
∵四边形ADFP是菱形,∠AED=45°,OA=OD,
∴AF⊥DP,∠AOD=90°,∠DAG=∠PEG,
∴∠AGE=90°,∠DAO=45°,
∴∠EAG=45°,∠DAG=∠PEG=22.5°,
∴∠EAD=∠DAG+∠GAE=22.5°+45°=67.5°,
故答案为:67.5°;
②∵四边形BFDP是正方形,
∴BF=FD=DP=PB,
∠DPB=∠PBF=∠BFD=∠FDP=90°,
∴此时点P与点O重合,
∴此时DE是直径,
∴∠EAD=90°,
故答案为:90°.
点评 本题考查菱形的判定与性质、切线的性质、正方形的判定,解答本题的关键是明确题意,找出所求问题需要的条件,利用菱形的性质和正方形的性质解答.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
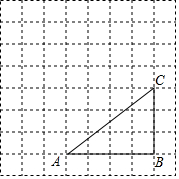 如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上.
如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
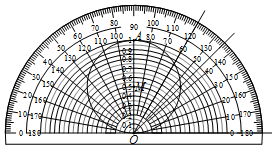 利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )| A. | 70° | B. | 50° | C. | 40° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3>|-7| | B. | $\sqrt{12}$>3$\sqrt{2}$ | C. | 0<-2 | D. | ($\frac{1}{2}$)2<3-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当两块三角板的斜边完全拼接在一起时,所拼成的图形一定是轴对称图形 | |
| B. | 当两块三角板的对应直角边完全拼接在一起时,所拼成的图形可能是等边三角形 | |
| C. | 当两块三角板可以通过平移后重合时,所拼成的图形不可能是轴对称图形 | |
| D. | 当两块三角板只有直角顶点拼接在一起时,所拼成的图形不可能是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
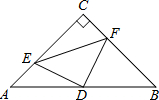 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com