
【题目】解下列方程或方程组:
(1)3x-(x-5)=2(2x-1);
(2)![]() ;
;
(3)![]() ;
;
(4) .
.
【答案】(1)x=![]() ;(2)y=
;(2)y=![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)先去括号,再移项,合并同类项,系数化为1即可得到方程的解;
(2)先去分母,再去括号、移项,合并同类项,系数化为1即可得到方程的解;
(3)根据加减法解方程组;
(4)先将方程组中的两个方程分别化简,再利用加减法解方程组.
(1)3x-(x-5)=2(2x-1),
3x-x+5=4x-2,
2x-4x=-2-5,
-2x=-7,
x=![]() ;
;
(2)![]() ,
,
3(y+2)-4(2y-1)=24,
3y+6-8y+4=24,
-5y=14,
y=![]() ;
;
(3)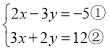 ,
,
①×2得:4x-6y=-10③,
②×3得:9x+6y=36④,
③+④得:13x=26,
解得x=2,
将x=2代入①得:4-3y=-5,
y=3,
∴原方程组的解是![]() ;
;
(4)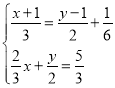 ,
,
将方程组化简得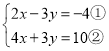 ,
,
①+②得:6x=6,
解得x=1,
将x=1代入②得:4+3y=10,
y=2,
∴原方程组的解是![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】校学生会体育部为更好的开展同学们课外体育活动,现对学生最喜欢的一项球类运动进行了随机抽样调查,根据调查的结果绘制成如图①和②所示的两幅不完整的统计图,其中 A.喜欢篮球 B.喜欢足球 C.喜欢乒乓球,D.喜欢排球,请你根据统计图提供的信息,完成下列问题:

(1)本次一共调查了 名学生;
(2)把图①汇总条形统计图补充完整;
(3)求图②中表示“D.喜欢排球”部分所在扇形的圆心角的度数;
(4)若该校有3000名学生,请你估计全校可能有多少名学生喜欢足球运动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).
(1)用列表法或树形图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率;
(3)小明、小华玩游戏,规则如下:组成数对和为偶数小明赢,组成数对和为奇数小华赢.你认为这个游戏公平吗?若不公平,请重新设计一个对小明、小华都公平的游戏.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A在y轴的正半轴上,点B在第二象限,AO=a,AB=b,BO与x轴正方向的夹角为150°,且a2b2+ab=0.

(1)试判定△ABO的形状;
(2)如图1,若BC⊥BO,BC=BO,点D为CO的中点,AC、BD交于E,求证:AE=BE+CE;
(3)如图2,若点E为y轴的正半轴上一动点,以BE为边作等边△BEG,延长GA交x轴于点P,问:AP与AO之间有何数量关系?试证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为190元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1770元 |
第二周 | 4台 | 10台 | 3060 元 |
(进价、售价均保持不变,利润=销售收入一进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5300元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②、图③是3×3的正方形网格,每个网格图中有3个小正方形己涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)在图①中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)在图②中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)在图③中选取2个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形.(请将三个小题依次作答在图①、图②、图③中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锦潭社区计划对某区域进行绿化,经投标,由甲、乙两个工程队一起来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用
区域的绿化时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天各能完成的绿化面积;
(2)若计划绿化的区域面积是![]() ,甲队每天绿化费用是
,甲队每天绿化费用是![]() 万元,乙队每天绿化费用为
万元,乙队每天绿化费用为![]() 万元.
万元.
①当甲、乙各施工几天,既能刚好完成绿化任务,又能使总费用恰好为![]() 万元;
万元;
②按要求甲队至少施工![]() 天,乙队至多施工
天,乙队至多施工![]() 天,当甲乙各施工几天,既能刚好完成绿化任务,又使得总费用最少(施工天数不能是小数)并求最少总费用.
天,当甲乙各施工几天,既能刚好完成绿化任务,又使得总费用最少(施工天数不能是小数)并求最少总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com