
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D. 
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=5,求⊙O的半径长.
【答案】
(1)证明:连结OC(如图所示),
则∠ACO=∠CAO (等腰三角形,两底角相等),
∵CD切⊙O于C,∴CO⊥CD,
又∵AD⊥CD,
∴AD∥CO.
∴∠DAC=∠ACO (两直线平行,内错角相等),
∴∠DAC=∠CAO,
∴AC平分∠BAD.
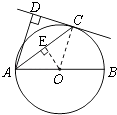
(2)过点E画OE⊥AC于E(如图所示),
在Rt△ADC中,AD= ![]() =6,
=6,
∵OE⊥AC,∴AE= ![]() ,AC=
,AC= ![]() ,
,
∵∠CAO=∠DAC,∠AEO=∠ADC=Rt∠,
∴△AEO∽△ADC,
∴ ![]() ,即:
,即: 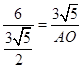 ,
,
∴AO= ![]() ,即⊙O的半径为
,即⊙O的半径为 ![]()
【解析】(1)根据等腰三角形的性质,可得∠ACO与∠CAO的关系,根据平行线的性质,可得∠DAC与∠ACO的关系,根据等量代换,可得答案;(2)连接BC,根据圆周角定理的推理得到∠ACB=90°,又∠DAC=∠OAC,由此可以得到△ADC∽△ACB,然后利用相似三角形的性质即可解决问题.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解南通市80万市民“获取新闻的最主要途径”,某市记者开展了一次调查,根据调查结果绘制了如下尚不完整的统计图.
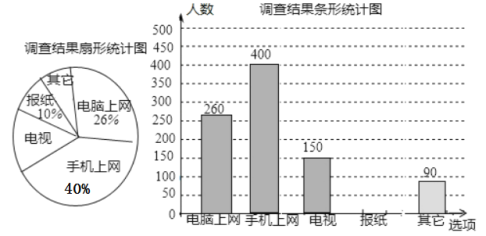
根据以上信息解答下列问题:
(1)这次调查适合采用_____________的调查方式(填“全面调查”或“抽样调查”);
(2)这次调查样本容量是____________.
(3)扇形统计图中,“电视”所对应的圆心角的度数是____________;
(4)条形统计图中“报纸”对应的人数是____________;
(5)南通市约有80万人,请估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.( ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).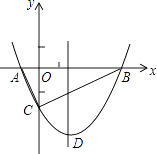
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
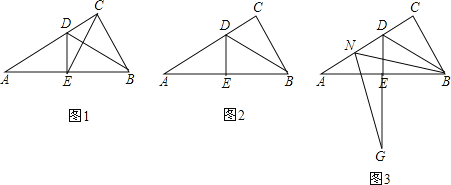
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
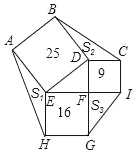
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,以AC为直径作 ![]() 交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是 ![]() 的切线;
的切线;
(2)若CF=2,DF=4,求 ![]() 直径的长.
直径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com