
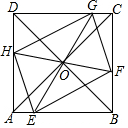
 如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.分析 (1)根据全等三角形的对应边相等,即可得出结论;
(2)根据相似三角形的对应边成比例,即可得出AE=AH,或AE+AH=1;
(3)根据△OPH∽△EPA,即可得到PH×PE=OP×AP,据此可得OP2+PH×PE=OP2+OP×AP=OP(OP+AP)=OP×OA,再根据△OPE∽△OEA,即可得到OP×OA=OE2,据此可得OP2+PH×PE=OE2,最后根据OE的最小值求得OP2+PH•PE的最小值.
解答  解:(1)如图所示,∵正方形ABCD,
解:(1)如图所示,∵正方形ABCD,
∴AO=CO,∠OAH=∠OCF=45°,
又∵∠AOH=∠COF,
∴△AOH≌△COF,
∴OH=OF;
故答案为:=;
(2)当四边形EFGH为矩形时,∠HEF=90°,
∴∠AEH+∠BEF=90°,
在正方形ABCD中,∠HAE=∠EBF=90°,
∴∠AEH+∠AHF=90°,
∴∠AHE=∠BEF,
∴△AEH∽△BFE,
∴$\frac{AE}{BF}$=$\frac{AH}{BE}$,
令AE=x,AH=y,则BF=1-y,BE=1-x,
∴$\frac{x}{1-y}$=$\frac{y}{1-x}$,
即x-y=x2-y2=(x+y)(x-y),
∴x=y或x+y=1,
∴AE=AH,或AE+AH=1;
(3)如图所示,当四边形EFGH为正方形时,∠HOE=90°,OH=OE,
∴∠OEH=∠OHE=45°,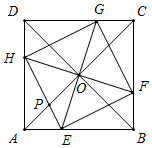
∴∠OHP=∠PAE=45°,
∵∠HPO=∠APE,
∴△OPH∽△EPA,
∴$\frac{PH}{AP}$=$\frac{OP}{PE}$,即PH×PE=OP×AP,
∴OP2+PH×PE=OP2+OP×AP=OP(OP+AP)=OP×OA,
∵∠OEP=∠OAE=45°,∠POE=∠EOA,
∴△OPE∽△OEA,
∴$\frac{OP}{OE}$=$\frac{OE}{OA}$,即OP×OA=OE2,
∴OP2+PH×PE=OE2,
∵当OE⊥AB时,OE最小,此时OE=$\frac{1}{2}$,
∴当OE=$\frac{1}{2}$时,OP2+PH×PE最小,且等于$\frac{1}{4}$.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,全等三角形的判定与性质以及正方形的性质的综合应用,解决问题的关键是依据相似三角形的对应边成比例,列式计算即可得出结论.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.


科目:初中数学 来源: 题型:选择题
 如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )
如图,点B、C把弧线AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=2,则图中阴影部分的面积是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下列材料:阅读下列材料:
阅读下列材料:阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2(x+1)2 | B. | y=-2(x+1)2+2 | C. | y=-2(x-1)2+2 | D. | y=-2(x-1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
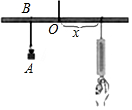 如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:
如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:| x(cm) | … | 10 | 15 | 20 | 25 | 30 | … |
| y(N) | … | 30 | 20 | 15 | 12 | 10 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com