Question

图1至图7的正方形霓虹灯广告牌ABCD都是20×20的等距网格（每个小方格的边长均为1个单位长），其对称中心为点O．
如图1，有一个边长为6个单位长的正方形EFGH的对称中心也是点O，它每秒1个单位长的速度由起始位置向外扩大（即点O不动，正方形EFGH经过一秒由6×6扩大为8×8；再经过一秒，由8×8扩大为10×10；…），直到充满正方形ABCD，再以同样的速度逐步缩小到起始时的大小，然后一直不断地以同样速度再扩大、再缩小．
另有一个边长为6个单位长的正方形MNPQ从如图1所示的位置开始，以每秒1个单位长的速度，沿正方形ABCD的内侧边缘按A?B?C?D?A移动（即正方形MNPQ从点P与点A重合位置开始，先向左平移，当点Q与点B重合时，再向上平移，当点M与点C重合时，再向右平移，当点N与点D重合时，再向下平移，到达起始位置后仍继续按上述方式移动）．
正方形EFGH和正方形MNPQ从如图1的位置同时开始运动，设运动时间为x秒，它们的重叠部分面积为y个平方单位．
（1）请你在图2和图3中分别画出x为2秒、18秒时，正方形EFGH和正方形MNPQ的位置及重叠部分（重叠部分用阴影表示），并分别写出重叠部分的面积；
（2）①如图4，当1≤x≤3.5时，求y与x的函数关系式；
②如图5，当3.5≤x≤7时，求y与x的函数关系式；
③如图6，当7≤x≤10.5时，求y与x的函数关系式；
④如图7，当10.5≤x≤13时，求y与x的函数关系式．
（3）对于正方形MNPQ在正方形ABCD各边上移动一周的过程，请你根据重叠部分面积y的变化情况，指出y取得最大值和最小值时，相对应的x的取值情况，并指出最大值和最小值分别是多少．

Answer 1

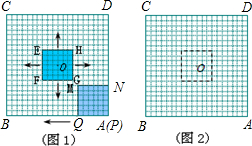
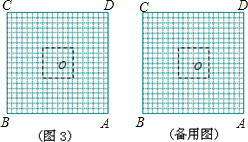
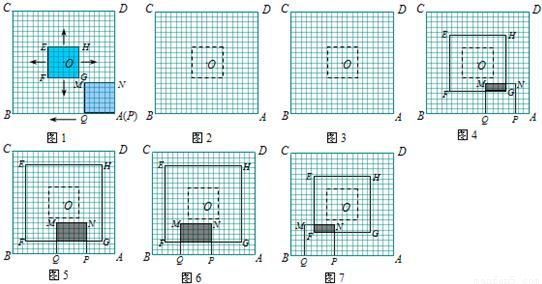
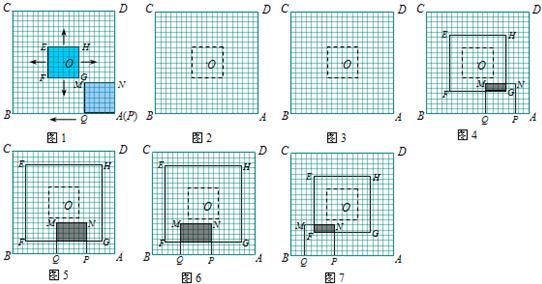
解：（1）相应的图形如图1，2．
当x=2时，y=3；
当x=18时，y=18．


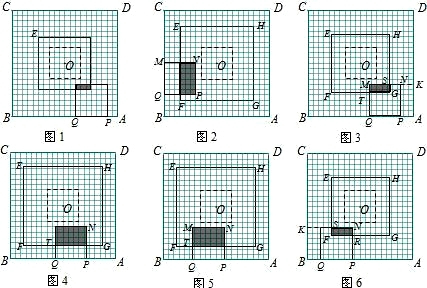
（2）①当1≤x≤3.5时，如图3，
延长MN交AD于K，
设MN与HG交于S，MQ与FG交于T，则MK=6+x，SK=TQ=7-x，从而MS=MK-SK=2x-1，MT=MQ-TQ=6-（7-x）=x-1．
∴y=MT•MS=（x-1）（2x-1）=2x²-3x+1．
②当3.5≤x≤7时，如图4，
设FG与MQ交于T，则
TQ=7-x，
∴MT=MQ-TQ=6-（7-x）=x-1．
∴y=MN•MT=6（x-1）=6x-6．
③当7≤x≤10.5时，如图5，
设FG与MQ交于T，则
TQ=x-7，
∴MT=MQ-TQ=6-（x-7）=13-x．
∴y=MN•MT=6（13-x）=78-6x．
④当10.5≤x≤13时，如图6，
设MN与EF交于S，NP交FG于R，延长NM交BC于K，则MK=14-x，SK=RP=x-7，
∴SM=SK-MK=2x-21，从而SN=MN-SM=27-2x，NR=NP-RP=13-x．
∴y=NR•SN=（13-x）（27-2x）=2x²-53x+351．

（3）对于正方形MNPQ，
①在AB边上移动时，当0≤x≤1及13≤x≤14时，y取得最小值0；
当x=7时，y取得最大值36．
②在BC边上移动时，当14≤x≤15及27≤x≤28时，y取得最小值0；
当x=21时，y取得最大值36．
③在CD边上移动时，当28≤x≤29及41≤x≤42时，y取得最小值0；
当x=35时，y取得最大值36．
④在DA边上移动时，当42≤x≤43及55≤x≤56时，y取得最小值0；
当x=49时，y取得最大值36．
分析：（1）当x=2时，Q离AD的距离为6+2=8，而G离AD的距离为7-2=5，因此重合部分的长为3．同理可求得重合部分的宽为1，因此y=3．
当x=18时，正方形MNPQ走完AB需14秒，因此x=18时，正方形MNPQ在BC边上运动了4秒，而正方形EHFG扩张到最大需7秒再缩小到原来的大小需7秒，因此x=18时，正方形EHFG重复第二次运动，且第二次运动过程中运动了4秒，因此MN离AB的距离为6+4=10，OP离AB的距离为4，因此重合部分的长为6，同理可求得重合部分的宽为3，y=3×6=18．
（2）①当1≤x≤3.5时，是正方形EHGF第一次向外扩张的过程，此时MK=x+6，SK=7-x，因此MS=2x-1．同理可求得SG的长，由此可得出重合部分的面积y与x的函数关系式．
②当3.5≤x≤7时，正方形EHGF第一次向内收缩，此时重合部分的长不变为MN的长即6，而EQ=x，NP=6，因此重合部分的宽为6-x，由此可得出y与x的函数关系式．
③当7≤x≤10.5时，正方形EHGF第二次向外扩张，此时重合部分的宽仍为MN的长即6，MQ=6，TQ=x-7，因此MT=13-x，由此可得出y与x的函数关系式．
④当10.5≤x≤13时，正方形EHGF第二次向内收缩，解法参照①．
（3）根据②中x不同区间的y的函数关系式，可根据各函数的性质和自变量的取值范围求出y的最大或最小值．
点评：本题为压轴题有一定难度，但难题也分层次性设计，只要平时多加积累解题经验，探解题规律，一定会有很大收获．
命题立意：考查解决大综合题的数学能力．