
(1)观察图中的各个角,寻找对顶角(不含平角):
①如图a中,共有_________对对顶角;
②如图b中,共有_________对对顶角;
③如图c中,共有_________对对顶角;
④探究①—③各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成_________对对顶角;
(2)若n条直线两两相交于不同的点时,可形成_________对对顶角.你能将上述两种情形归纳一下吗?

(1)①2 ②6 ③12 ④n(n-1) (2)n(n-1) 归纳结论:n条直线两两相交,共形成n(n-1)对对顶角.
【解析】解:本题考查了对等角的性质和观察总结能力。
⑴、①中对等角是∠AOC与∠BOD, ∠AOD与∠BOC; ②中对等角是∠AOC与∠DOB, ∠COF与DOE, ∠BOF与∠AOE, ∠AOE∠与BOE, ∠BOC与∠AOD, ∠DOF与∠COE;③中是4条线交于O点对等角的数目是在6对对等角的基础上加上第四条线与前3条线的2个端点的组合共6对对等角所以③中对等角共有12对; ④根据以上总结2条线相交对等角有2*(2-1)=4;3条线相交对等角4+2*2=6;4条线相交对等角6+3*2=12;以此类推2*0+2*(2-1)+…+2*(n-1)=2*(0+1+2+3+…+n-1)= 2*[ (n-1+0)*n/2]=n*(n-1);n>0,n为整数。
⑵两条直线相交共形成2对对等角,n条直线两两相交于不同的点共有[(n-1)+(n-2)+(n-3)+…+3+2+1]对两条直线相交的情况,所以n条直线两两相较于不同的]点共有对等角[(n-1)+(n-2)+(n-3)+…+3+2+1]*2=[﹙n-1+1﹚*﹙n-1﹚/2]*2=n*(n-1) ;n>0,n为整数


科目:初中数学 来源: 题型:044
观察统计图,回答问题.
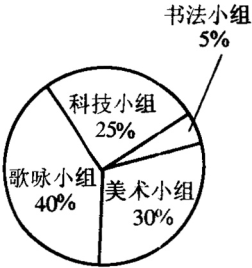
(1)哪种课外活动最受欢迎?
(2)哪两种课外活动受欢迎的程度比较接近?
(3)最受欢迎的两种课外活动是指什么?它们的百分比之和是多少?
(4)图中的各个扇形分别代表了什么?
(5)你认为图中的各个百分比是如何得到的、所有的百分比之和是多少?
(6)如果你是班级的班长,准备组织一次课外活动小组的学习汇报,在选定节目时,应如何分配节目比例?
(7)你还能从图中获取什么信息?
(8)你能从图中,计算得出年级参加课外活动小组的人数吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com