
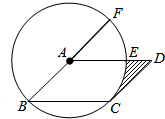
 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π. 分析 连结AC,如图,设半径为r,先根据切线的性质得∠ACD=90°,再根据平行四边形的性质得AB∥CD,AD∥BC,则∠CAF=90°,∠1=∠B,∠2=∠3,利用∠B=∠3易得∠1=∠2=45°,则根据弧长公式可得$\frac{45π×r}{180}$=π,解得r=4,然后根据扇形面积公式,利用S阴影部分=S△ACD-S扇形CAE进行计算即可.
解答 解:连结AC,如图,设半径为r,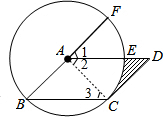
∵AB的长为半径的圆恰好与CD相切于点C,
∴AC⊥CD,
∴∠ACD=90°,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠CAF=90°,∠1=∠B,∠2=∠3,
而AB=AC,
∴∠B=∠3,
∴∠1=∠2=45°,
∵$\widehat{EF}$的长为π,
∴$\frac{45π×r}{180}$=π,解得r=4,
在Rt△ACD中,∵∠2=45°,
∴AC=CD=4,
∴S阴影部分=S△ACD-S扇形CAE=$\frac{1}{2}$×4×4-$\frac{45π×{4}^{2}}{360}$=8-2π,
故答案为:8-2π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平行四边形的性质和扇形的面积公式.


科目:初中数学 来源: 题型:解答题
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧的长度(cm) | 8 | 8.5 | 9 | 9.5 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
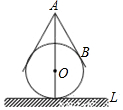 用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.
用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积$\frac{7\sqrt{3}}{2}$.
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积$\frac{7\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
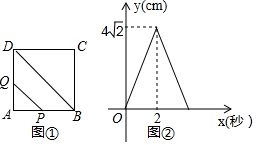
| A. | $2\sqrt{2}cm$ | B. | $3\sqrt{2}cm$ | C. | $4\sqrt{2}cm$ | D. | $5\sqrt{2}cm$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
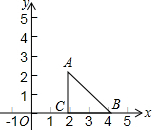 如图,在平面直角坐标系中,等腰直角三角形△ABC的腰长是2,写出一个函数y=$\frac{k}{x}$(k≠0),是它的图象与△ABC有公共点,这个函数表达式为y=$\frac{4}{x}$(答案不唯一).
如图,在平面直角坐标系中,等腰直角三角形△ABC的腰长是2,写出一个函数y=$\frac{k}{x}$(k≠0),是它的图象与△ABC有公共点,这个函数表达式为y=$\frac{4}{x}$(答案不唯一).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com