
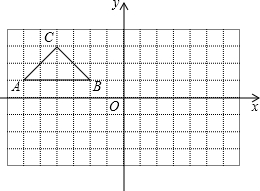
 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;| 22+22 |
| 2 |
| 2 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
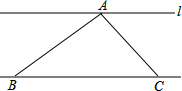 如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )
如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )| A、向直线l的上方运动 |
| B、向直线l的下方运动 |
| C、在直线l上运动 |
| D、以上三种情形都可能发生 |
查看答案和解析>>
科目:初中数学 来源: 题型:
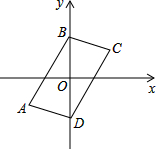 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交 |
| AB |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
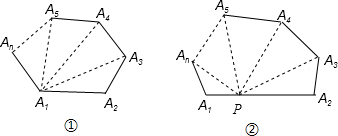
 如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.
如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com