
 如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?
如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗? 分析 利用三个正方形的面积可得出相当于三角形三边的平方,进而利用74=52+72,116=42+102,370=92+172,利用勾股定理的逆定理求出即可.
解答  解:∵74=52+72,
解:∵74=52+72,
∴AB是两直角边分别为5和7的直角三角形的斜边,做出这个直角三角形,得Rt△ABE,
同理,作Rt△BCF,其中BF=4,FC=10,延长AE、CF交于D,则AD=9,CD=17,
而AC2=370=92+172=AD2+CD2,
∴△ACD是直角三角形,∠ADC=90°,
∴S△ABC=S△ADC-S△AEB-S△BCF-S四边形EDFB
=$\frac{1}{2}$×17×9-$\frac{1}{2}$×7×5-$\frac{1}{2}$×10×4-4×7
=11.
即池塘的面积为11英亩.
点评 此题主要考查了勾股定理的应用,关键是运用勾股定理和其逆定理构造出新图形,用构造法解题的思想,有助于提高运用数学知识解决实际问题的能力.


科目:初中数学 来源: 题型:填空题
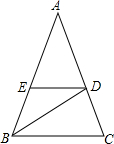 顶角为36°的等腰三角形被叫做“黄金三角形”,如图所示,△ABC为顶角为36°等腰三角形.BD为∠ABC的平分线,过点D作BC的平行线交AB于点E
顶角为36°的等腰三角形被叫做“黄金三角形”,如图所示,△ABC为顶角为36°等腰三角形.BD为∠ABC的平分线,过点D作BC的平行线交AB于点E 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
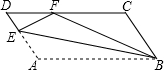 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处.若△FDE的周长为5,△FCB的周长为17,则FC的长为6.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处.若△FDE的周长为5,△FCB的周长为17,则FC的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C且与AB交于点D.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C且与AB交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com