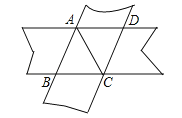
【题目】如图所示，将两条等宽的纸条重叠在一起，得到四边形
，若
，则
___.
【答案】
【解析】分析：首先可证明ABCD是菱形，再由∠ABC=60°和菱形的性质可得△ABC是等边三角形，得AC=AB=8，再由菱形的面积=底×高=对角线乘积÷2即可得到结论．
详解：如图，作BE⊥AD于点E，BF⊥DC于点F，由题意知，纸条等宽，即有：BE=BF，∵AE∥BC，∴∠EAB=∠ABC，∵AB∥FC，∴∠ABC=∠FCB，又∵BE=BF，∠AEB=∠BFC=90°，∴△AEB≌△CFB（ASA），∴AB=BC，∵∠ABC=60°，
∴△ABC是等边三角形，∴AC=AB=8．
∵AD∥BC，∴∠EAB=∠ABC=60°，∴∠EBA=30°，∴AE=4,BE=
AE=
.
∵S四边形ABCD=AD×BE=
AC×BD，∴BD=
=.
小学教材完全解读系列答案科目：初中数学 来源： 题型：
【题目】某校门前正对一条公路，车流量较大，为便于学生安全通过，特建一座人行天桥．如图，是这座天桥的引桥部分示意图，上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成．已知∠A=37°，天桥高度DH为5.1米，引桥水平跨度AH为8.3米．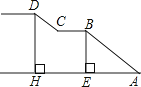
（1）求水平平台BC的长度；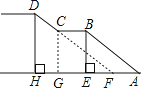
（2）若两段楼梯AB：CD=10：7，求楼梯AB的水平宽度AE的长．
（参考数据：sin37°≈ 
，cos37°≈ 
，tan37°≈ 
）
查看答案和解析>>
科目：初中数学 来源： 题型：
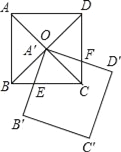
【题目】已知，如图，正方形ABCD的对角线AC，BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，A′B′交BC于点E，A′D′交CD于点F．
（1）求证：OE=OF；
（2）若正方形ABCD的对角线长为4，求两个正方形重叠部分的面积为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作直线DE垂直BC于F，且交BA的延长线于点E．
（1）求证：直线DE是⊙O的切线；
（2）若cos∠BAC= 
，⊙O的半径为6，求线段CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在我县中小学读书活动中，某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动，将图书分为甲、乙、丙、丁四类，学生可根据自己的爱好任选其中一类，学校根据调查情况进行了统计，并绘制了不完整条形统计图和扇形统计图．
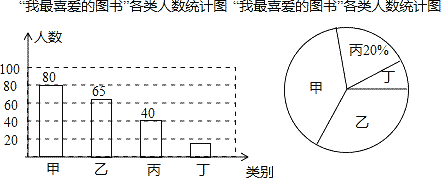
请你结合图中的信息，解答下列问题（其中（1）、（2）直接填答案即可）；
（1）本次调查了 名学生；
（2）被调查的学生中，最喜爱丁类图书的有 人，最喜爱甲类图书的人数被调查人数的 %．
（3）在最喜爱丙类图书的学生中，女生人数是男生人数的1.5倍，若这所学校约有学生1800人，请你估计该校最喜爱丙类图书的女生和男生分别有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2016次运动后，动点P的坐标是（ ）
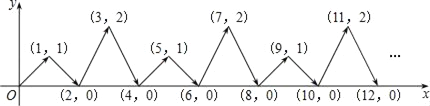
A. （2016，1） B. （2016，0） C. （2016，2） D. （2017，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若∠DAE=50°°,则∠BAC=________,若△ADE的周长为19cm,则BC=_____cm.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有若干个数，第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为an，若a1=
，从第二个数起，每个数都等于“1与它前面那个数差的倒数”.
(1)计算：a2 ，a3 ，a4 ，a5的值；
(2)这排数有什么规律？由你发现的规律，计算a2014的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
