(1)证明:∵PC⊥CD,AB为⊙O的直径,
∴∠DCP=∠ACB=∠ADB=90°,
∵∠DCP=∠ACD+∠ACP,∠ACB=∠ACP+∠BCP,
∴∠ACD=∠BCP,
∵AC=BC,且∠ACB=90°,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴∠BDC=∠BAC=45°,
∴△DCP是等腰直角三角形
∴DC=PC,又∠ACD=∠BCP,AC=BC,
∴△ADC≌△BPC,
∴AD=BP;(3分)
(2)证明:∵∠ABD=∠ACD,
∴

∴
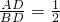
,∴

,
∴P是BD的中点,(5分)
∴AD=PB=PD,
∴△ADP是等腰直角三角形,
∴∠APD=45°,又∠BDC=45°,
∴∠APD=∠BDC,
∴DC∥AP;
(3)解:∵△ADC≌△BPC,∴S
△ACD=S
△BCP,
又∵S
△ABP=S
△ADP,△ADP为等腰直角三角形,AD=DP=x,
∴S
△ADP=
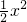
,
∵
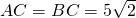
,△ABC为等腰直角三角形,
∴S
△ABC=

×5

×5

=25,
则y=S
△ACP+S
△ACD=S
△ACP+S
△BCP
=S
△ABC-S
△ABP
=S
△ABC-S
△ADP
=

(

)
分析:(1)根据PC与CD垂直,由垂直定义得到∠PCD为直角,又AB为圆的直径,由直径所对的圆周角为直角得到∠ACB与∠ADB也为直角,根据同角的余角相等得到∠ACD与∠BCP相等,又AC=BC得到三角形ABC为等腰直角三角形,进而得到∠CAB=45°,根据同弧所对的圆周角相等得到∠CDP=45°,即三角形DCP为等腰直角三角形,所以CD=CP,利用”SAS“即可得到三角形ACD与三角形BCP全等,根据全等三角形的对应边相等得到AD=PB;
(2)根据同弧所对的圆周角相等得到∠ABD=∠ACD,则tan∠ACD=tan=∠ABD,在直角三角形ABD中,由正切函数定义得到AD等于BD的一半,由(1)得到AD=PB代入比例式得到P为BD中点,即AP为直角三角形ABD斜边上的中线,则AP=DP,所以三角形ADP为等腰直角三角形,所以∠APD=45°,又∠CDP=45°,得到一对内错角相等,从而得到两直线平行,得证;
(3)四边形APBC的面积可以分为三角形ACD和三角形APC的面积之和,而三角形ACD与三角形BCP全等,故四边形的面积可以等于三角形BCP和三角形APC的面积之和,即三角形ABC的面积减去三角形ABP的面积,而P为BD中点,根据等底同高得到三角形ABP的面积与三角形ADP的面积相等,从而得到四边形的面积等于三角形ABC的面积减去三角形ADP的面积,然后由这两个三角形都为等腰直角三角形且直角边分别为5

和x,利用三角形的面积公式即可表示出y与x的函数关系式,同时求出自变量x的范围.
点评:此题考查了圆周角定理,全等三角形的判定与性质,等腰直角三角形的判定与性质,以及面积的变换与求法.此题的综合性比较强,难度比较大,在解题时充分利用以上相关知识来考虑,在对全等三角形进行证明时,关键是找出对应相等的量,在圆中要关注圆周角,等弧,等弦这些相关量,要注意建立和加强知识间的纵向联系和横向联系,建立良好的知识结构体系,从而更好的提取知识,应用知识,发展数学思维.

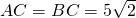 ,点D是
,点D是 上一个动点,连接AD、CD和BD,BD与AC相交于点E,过点C作PC⊥CD于C,PC与BD相交于点P,连接OP和AP.
上一个动点,连接AD、CD和BD,BD与AC相交于点E,过点C作PC⊥CD于C,PC与BD相交于点P,连接OP和AP.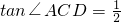 ,求证:DC∥AP;
,求证:DC∥AP;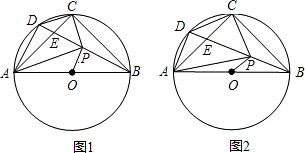

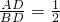 ,∴
,∴ ,
,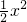 ,
, ,△ABC为等腰直角三角形,
,△ABC为等腰直角三角形, ×5
×5 ×5
×5 =25,
=25, (
( )
) 和x,利用三角形的面积公式即可表示出y与x的函数关系式,同时求出自变量x的范围.
和x,利用三角形的面积公式即可表示出y与x的函数关系式,同时求出自变量x的范围.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案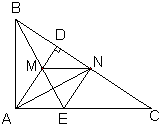 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.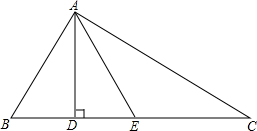 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.