
 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点M是线段AB上的一个动点(点A、B除外),点N在x轴上方,使得以O、B、M、N为顶点的四边形是菱形,点N的坐标为($\frac{144}{25}$,$\frac{192}{25}$)或(-4,3).
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点M是线段AB上的一个动点(点A、B除外),点N在x轴上方,使得以O、B、M、N为顶点的四边形是菱形,点N的坐标为($\frac{144}{25}$,$\frac{192}{25}$)或(-4,3). 分析 分两种情形讨论①OB为边,②OB为对角线,分别求出点N坐标即可.
解答 解:如图,当OB为边时,四边形OBNM是菱形,连接ON交AB于H,延长NM交OA于E,
∵$\frac{1}{2}$OA×OB=$\frac{1}{2}$OH•AB,
∴OH=$\frac{24}{5}$,BH=HM=$\frac{18}{5}$,
∴AM=AB-2BH=$\frac{14}{5}$,
由EM∥OB,得到$\frac{EM}{OB}$=$\frac{AM}{AB}$=$\frac{AE}{AO}$,
∴EM=$\frac{42}{25}$,AE=$\frac{56}{25}$,
∴OE=$\frac{144}{25}$,
∴点N坐标($\frac{144}{25}$,$\frac{192}{25}$),
如图当OB为对角线时,易知点N坐标(-4,3).
综上所述以O、B、M、N为顶点的四边形是菱形,点N的坐标为($\frac{144}{25}$,$\frac{192}{25}$)或(-4,3).
点评 本题考查一次函数图象上的点坐标特征,菱形的性质等知识,解题的关键是学会分类讨论,注意不能漏解,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届广东省佛山市顺德区九年级第一次模拟考试数学试卷(解析版) 题型:单选题
已知二次函数 的图象与x轴有交点,则k的取值范围是( )
的图象与x轴有交点,则k的取值范围是( )
A. 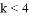 B.
B.  C.
C. 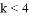 且
且 D.
D.  且
且
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
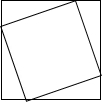 一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )
一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )| A. | $\sqrt{58}$ | B. | $\frac{7}{2}$$\sqrt{5}$ | C. | 8 | D. | $\sqrt{65}$ | ||||
| E. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,工人师傅现在需要把一块三角形的铁板,通过切割焊接成一个与其面积相等的平行四边形,你能帮助他设计一种可行的方案吗?请在图中画出焊接线,并说明你的理由.
如图,工人师傅现在需要把一块三角形的铁板,通过切割焊接成一个与其面积相等的平行四边形,你能帮助他设计一种可行的方案吗?请在图中画出焊接线,并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
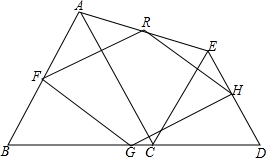 如图,点C是线段BD上的一点,△ABC和△CDE为等边三角形,点F、G、H、R分别为四边形ABDE各边的中点.
如图,点C是线段BD上的一点,△ABC和△CDE为等边三角形,点F、G、H、R分别为四边形ABDE各边的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com