
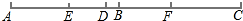 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长. 分析 如图,设BD=x,则AB=4x,CD=5x,根据线段中点的定义得AE=BE=2x,DF=CF=2.5x,则DE=BE-BD=x,EF=DE+DF=3.5x,于是可得到方程3.5x=20,解得x=$\frac{40}{7}$,则BD=$\frac{40}{7}$
解答 解:如图,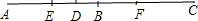 设BD=x,则AB=4x,CD=5x,
设BD=x,则AB=4x,CD=5x,
∵E、F分别为线段AB、CD的中点,
∴AE=BE=$\frac{1}{2}$AB=2x,DF=CF=$\frac{1}{2}$CD=2.5x,
∴DE=BE-BD=2x-x=x,
∴EF=DE+DF=x+2.5x=3.5x,即3.5x=20,解得x=$\frac{40}{7}$,
∴BD=$\frac{40}{7}$.
点评 本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.注意强调最后的两个字“长度”,也就是说,距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.常用代数式计算距离.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10000万精确到万位 | B. | 2.580精确到千分位 | ||
| C. | 0.0250有3个有效数字 | D. | 17049保留3个有效数字为1.71×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | x=$\frac{4}{9}$ | C. | x=-1 | D. | x=-$\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com