练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠ACB＝90°，D是BC的中点，DE⊥BC，CE//AD，若AC＝2，CE＝4，则四边形ACEB的周长为 ▲ ．

    【答案】10+．

    【解析】

    先证明四边形ACED是平行四边形，可得DE=AC=2．由勾股定理和中线的定义可求AB和EB的长，从而求出四边形ACEB的周长．

    ∵∠ACB=90°，DE⊥BC，∴AC∥DE．

    又∵CE∥AD，∴四边形ACED是平行四边形．∴DE=AC=2．

    在Rt△CDE中，DE= 2，CE＝4，由勾股定理得．

    ∵D是BC的中点，∴BC=2CD=4．

    在△ABC中，∠ACB=90°，由勾股定理得．

    ∵D是BC的中点，DE⊥BC，∴EB=EC=4．

    ∴四边形ACEB的周长=AC+CE+EB+BA=10+．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（11分）如图，抛物线y=ax2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且经过点（2，﹣3a），对称轴是直线x=1，顶点是M．

    （1）求抛物线对应的函数表达式；

    （2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；

    （3）设直线y=﹣x+3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；

    （4）当E是直线y=﹣x+3上任意一点时，（3）中的结论是否成立（请直接写出结论）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用“”规定一种新运算：对于任意有理数a和b，规定ab＝ab+2ab+a． 如：13＝1×3+2×1×3+1＝16

    （1）求3（﹣1）的值；

    （2）若（a+1）2＝36，求a的值；

    （3）若m＝2x，n＝（x）3（其中x为有理数），试比较m、n的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为丰富学生课余生活，我校准备开设兴趣课堂．为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况，在全校进行随机抽样调查，并根据收集的数据绘制了下面两幅统计图（信息尚不完整），请根据图中提供的信息，解答下面的问题：

    （1）此次共调查了多少名同学？

    （2）将条形图补充完整，并计算扇形统计图中乐器部分的圆心角的度数；

    （3）如果我校共有1000名学生参加这4个课外兴趣小组，而每个教师最多只能辅导本组的25名学生，估计书法兴趣小组至少需要准备多少名教师？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，矩形ABCD中，AB＝4，BC＝m（m＞1），点E是AD边上一定点，且AE＝1．

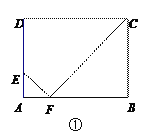
    （1）当m＝3时，AB上存在点F，使△AEF与△BCF相似，求AF的长度．

    （2）如图②，当m＝3.5时．用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F．（不写作法，保留作图痕迹）

    （3）对于每一个确定的m的值，AB上存在几个点F，使得△AEF与△BCF相似？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填空并解答：

    规定：a2＝a×a，a3＝a×a×a，an＝a×a×…×a（n 个 a）

    (1)（2×3）2＝ ，22×32＝ ，你发现（2× 3）2 的值与 22×32 的值 ．

    (2)（2×3）3＝ ，23×33＝ ，你发现（2×3）3 的值与 23×33 的值 ．

    由此，我们可以猜想：（a×b）2 a2×b2，（a×b）3 a3×b3，…（a×b）n an×bn.

    (3)利用(2)题结论计算（﹣2）2018×（﹣）2019 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

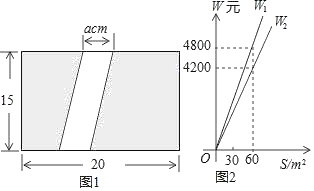
    【题目】如图1，为美化校园环境，某校计划在一块长为20m，宽为15m的长方形空地上修建一条宽为a（m）的甬道，余下的部分铺设草坪建成绿地．

    （1）甬道的面积为　 　m2，绿地的面积为　 　m2（用含a的代数式表示）；

    （2）已知某公园公司修建甬道，绿地的造价W1（元），W2（元）与修建面积S之间的函数关系如图2所示．①园林公司修建一平方米的甬道，绿地的造价分别为　 　元，　 　元．②直接写出修建甬道的造价W1（元），修建绿地的造价W2（元）与a（m）的关系式；③如果学校决定由该公司承建此项目，并要求修建的甬道宽度不少于2m且不超过5m，那么甬道宽为多少时，修建的甬道和绿地的总造价最低，最低总造价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嘉嘉将长为20cm，宽为10cm的长方形白纸，按图所示方法粘合起来，粘合部分（图上阴影部分）的宽为3cm．

    （1）求5张白纸粘合后的长度；

    （2）设x张白纸粘合后总长为ycm．写出y与x之间的函数关系式；

    （3）求当x=20时的y值，并说明它在题目中的实际意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一个平台远处有一座古塔，小明在平台底部的点C处测得古塔顶部B的仰角为60°，在平台上的点E处测得古塔顶部的仰角为30°．已知平台的纵截面为矩形DCFE，DE=2米，DC=20米，求古塔AB的高（结果保留根号）

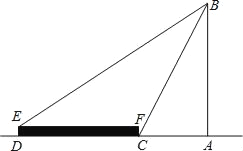
    查看答案和解析>>

    同步练习册答案