
 ��ͼ����֪������y=ax2+bx-3��ֱ��y=x����A��B���㣬��A��B����ĺ�����ֱ�Ϊ-1��3��
��ͼ����֪������y=ax2+bx-3��ֱ��y=x����A��B���㣬��A��B����ĺ�����ֱ�Ϊ-1��3������ ��1�������������A��B�������꣬���ô���ϵ�������ɽ�����⣮
��2����M��m��m2-m-3������H��m��m������MH��y�ᣬ��AB��H������S��MOB=S��MHO+S��MHB�������κ��������ö��κ��������ʽ�����⼴�ɣ�
��3��������ͼ��M��AB��ƽ���߽���������P1��P2���P1OB�͡�P2OB���MOB�����ȣ�������M����ԭ��ĶԳƵ�M�䣨-1��3������M��ƽ��AB��ֱ�ߵĽ���ʽΪy=x+4����ֱ���������߽���P3��P4�����P3OB�͡�P4OB���MOB�����ȣ����÷�����ֱ����P�����꼴�ɣ�
��� �⣺��1���������֪A��-1��-1����B��3��3����
��A��-1��-1����B��3��3������y=ax2+bx-3��$\left\{\begin{array}{l}{a-b-3=-1}\\{9a+3b-3=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$��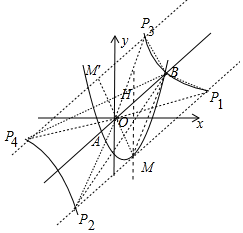
�������ߵĽ���ʽΪy=x2-x-3��
�跴���������Ľ���ʽΪy=$\frac{k}{x}$����B��3��3�������k=9��
�෴������������ʽΪy=$\frac{9}{x}$��
��2����M��m��m2-m-3������H��m��m������MH��y�ᣬ��AB��H��
��S��MOB=S��MHO+S��MHB��
��S��MOB=$\frac{1}{2}$•��m-m2+m+3��•3=-$\frac{3}{2}$��m-1��2+2��
��-$\frac{3}{2}$��0��
��m=1ʱ����MOB��������������ֵΪ2��
��ʱM��1��-3����
��3����ͼ��M��AB��ƽ���߽���������P1��P2���P1OB�͡�P2OB���MOB�����ȣ�
��ֱ��AB�Ľ���ʽΪy=x��M��1��-3����
��ֱ��P1P2�Ľ���ʽΪy=x-4��
��$\left\{\begin{array}{l}{y=x-4}\\{y=\frac{9}{x}}\end{array}\right.$���$\left\{\begin{array}{l}{x=2+\sqrt{13}}\\{y=\sqrt{13}-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=2-\sqrt{13}}\\{y=-6-\sqrt{13}}\end{array}\right.$��
��P1��2+$\sqrt{13}$��$\sqrt{13}$-2����P2��2-$\sqrt{13}$��-6-$\sqrt{13}$����
��M����ԭ��ĶԳƵ�M�䣨-1��3����
��M��ƽ��AB��ֱ�ߵĽ���ʽΪy=x+4����ֱ���������߽���P3��P4�����P3OB�͡�P4OB���MOB�����ȣ�
��$\left\{\begin{array}{l}{y=x+4}\\{y=\frac{9}{x}}\end{array}\right.$���$\left\{\begin{array}{l}{x=-2+\sqrt{13}}\\{y=2+\sqrt{13}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2-\sqrt{13}}\\{y=2-\sqrt{13}}\end{array}\right.$��
��P3��-2+$\sqrt{13}$��2+$\sqrt{13}$����P4��-2-$\sqrt{13}$��2-$\sqrt{13}$����
�������������������ĵ�P����Ϊ��2+$\sqrt{13}$��$\sqrt{13}$-2����2-$\sqrt{13}$��-6-$\sqrt{13}$����-2+$\sqrt{13}$��2+$\sqrt{13}$����-2-$\sqrt{13}$��2-$\sqrt{13}$����
���� ���⿼����κ����ۺ��⡢һ�κ����������������������������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ע�⿼������Ҫȫ�棬����©�⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮


 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
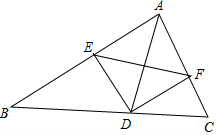 ��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ADC�ĸߣ�����˵������ȷ���У���������
��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ADC�ĸߣ�����˵������ȷ���У���������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 5�� | C�� | 4�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
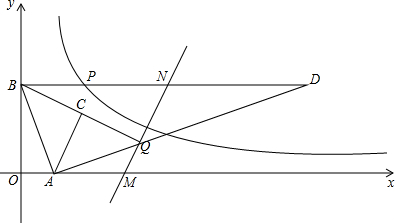
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
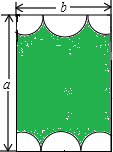 ��ͼ��һ�鳤Ϊa����Ϊb�ij����β�ƺ�����¿��ٵĻ��������ɵȰ뾶�������ķ�֮һԲ��һ����Բ��ɣ���ô�м��ƺ������ǣ�������
��ͼ��һ�鳤Ϊa����Ϊb�ij����β�ƺ�����¿��ٵĻ��������ɵȰ뾶�������ķ�֮һԲ��һ����Բ��ɣ���ô�м��ƺ������ǣ�������| A�� | ab-��b2 | B�� | ab-$\frac{��}{2}$b2 | C�� | ab-$\frac{��}{4}$b2 | D�� | ab-$\frac{��}{8}$b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�������� | B�� | һ�������� | C�� | ���������� | D�� | һ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com