

分析 (1)根据$\widehat{AB}$=$\widehat{BC}$,得到AB=BC,根据弦切角定理求出∠EAB=∠EBA=∠FCB=∠FBC,证明△AEB≌△CFB,得到答案;
(2)连接AC,作DG⊥AC于G,AH⊥DF于H,证明∠DAG=∠ABC,表示出AD、CD、AH的长,得到答案.
解答 解: (1)连接AC,
(1)连接AC,
∵$\widehat{AB}$=$\widehat{BC}$,
∴AB=BC,∠EAB=∠EBA=∠FCB=∠FBC,
∴△AEB≌△CFB,
∴BE=BF;
(2)连接AC,作DG⊥AC于G,AH⊥DF于H,
∵DE、DF是⊙O的切线,切点分别为A,C,
∴∠ABC=∠DAC=∠DCA,
∴AD=DC,
∴AG=CG=$\frac{1}{2}$AC,
∴tan∠DAG=tan∠ABC=$\frac{DG}{AG}$=$\frac{4}{3}$,
设DG=4k,则AG=3k,
∴AC=2AG=6k,AD=CD=5k,
$\frac{1}{2}$×AC×DG=$\frac{1}{2}$×CD×AH,
∴AH=$\frac{24}{5}$k,
∴sin∠EDF=$\frac{AH}{AD}$=$\frac{24}{25}$.
点评 本题考查的是三角形的内切圆的知识,掌握弦切角定理、切线长定理和锐角三角函数的概念是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
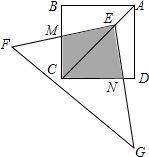 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )| A. | $\frac{5}{9}$a2 | B. | $\frac{4}{9}$a2 | C. | $\frac{2}{3}$a2 | D. | $\frac{1}{4}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量y(件) | 500 | 490 | 480 | 470 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
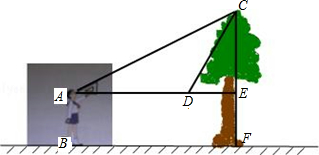 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com