
 ��ͼ���ڳ�����ABCD�У�AB=6cm��BC=8cm������P�ӵ�A��������3cm/s���ٶ�����ʱ�뷽�������˶�������P�˶�����Aʱ���˶�ֹͣ�����P�˶���ʱ��Ϊt��s����
��ͼ���ڳ�����ABCD�У�AB=6cm��BC=8cm������P�ӵ�A��������3cm/s���ٶ�����ʱ�뷽�������˶�������P�˶�����Aʱ���˶�ֹͣ�����P�˶���ʱ��Ϊt��s�������� �ٸ���·��=�ٶȡ�ʱ�����߶εij��ȼ��ɵó����ۣ��ٸ��ݵ�P���ڵ�λ�ü��ɵó�����t��һԪһ�β���ʽ����֮���ɵó�t��ȡֵ��Χ��
����$\frac{1}{2}$AB•BC��ֵ�ɵó�����P���߶�BC��DA��ʱ�����С�ABP�����Ϊ9cm2���ֵ�P���߶�BC��DA��������������������ε������ʽ���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��� �⣺�ٵ���P���߶�AB���˶�ʱ��AP=3t��
��ʱ0��3t��6����0��t��2��
����P�˶����߶�BC��ʱ��BP=3t-6��
��ʱ0��3t-6��8����2��t��$\frac{14}{3}$��
����P�˶����߶�DA��ʱ��AP=2����6+8��-3t=-3t+28��
��ʱ0��-3t+28��8����$\frac{20}{3}$��t��$\frac{28}{3}$��
�ʴ�Ϊ��3t��0��t��2����3t-6��2��t��$\frac{14}{3}$����-3t+28��$\frac{20}{3}$��t��$\frac{28}{3}$����
�ڡ�$\frac{1}{2}$AB•BC=$\frac{1}{2}$��6��8=24��24��9��
�൱��P���߶�BC��DA��ʱ�����С�ABP�����Ϊ9cm2��
����P���߶�BC��ʱ����$\frac{1}{2}$AB•BP=$\frac{1}{2}$��6��3t-6��=9��
��ã�t=3��
����P���߶�DA��ʱ����$\frac{1}{2}$AB•AP=$\frac{1}{2}$��6��-3t+28��=9��
��ã�t=$\frac{25}{3}$��
�൱tΪ3���$\frac{25}{3}$��ʱ����ABP�����Ϊ9cm2��
���� ���⿼����һԪһ�η��̵�Ӧ�á��д���ʽ�Լ���һԪһ�β���ʽ������Ĺؼ��ǣ��ٸ���������ϵ�г�����ʽ���ڸ��������ε�����г�����t��һԪһ�η��̣�


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | xy2 | B�� | ��xy | C�� | x3y | D�� | 3xy |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
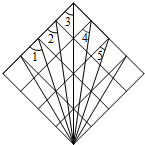 ��ͼΪ4��4������������ͼ�е��߶ξ�Ϊ����߶Σ��߶εĶ˵�Ϊ��㣩�����1+��2+��3+��4+��5�Ķ���Ϊ225�㣮
��ͼΪ4��4������������ͼ�е��߶ξ�Ϊ����߶Σ��߶εĶ˵�Ϊ��㣩�����1+��2+��3+��4+��5�Ķ���Ϊ225�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| 1 | 2 | 3 | 4 | �� |
| 2 | 4 | 6 | 8 | �� |
| 3 | 6 | 9 | 12 | �� |
| 4 | 8 | 12 | 16 | �� |
| �� | �� | �� | �� | �� |
| 10 | |
| a | |
| 21 |
| A�� | 16 | B�� | 18 | C�� | 20 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | |a+b|��ֵһ�������� | B�� | a2+1��ֵһ�������� | ||
| C�� | ��a��bʱ��a2��b2 | D�� | ��a��bʱ��|a|��|b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com