
【题目】在矩形ABCD中,AB=6,BC=12,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C,D的对应点分别为C′,D′,折痕与边AD交于点F,当点B,C′,D′恰好在同一直线上时,AF的长为_____.
【答案】8+![]() 或8﹣
或8﹣![]() .
.
【解析】分析: 由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,在Rt△BC′E中,由![]() =2,得到∠C′BE=30°,①当点C′在BC的上方时,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形根据等边三角形的性质和矩形的性质,即可得到AF的长;②当点C′在BC的下方时,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质,即可得到AF的长.
=2,得到∠C′BE=30°,①当点C′在BC的上方时,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形根据等边三角形的性质和矩形的性质,即可得到AF的长;②当点C′在BC的下方时,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质,即可得到AF的长.
详解: 由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,
∵点B、C′、D′在同一直线上,
∴∠BC′E=90°,
∵BC=12,BE=2CE,
∴BE=8,C′E=CE=4,
在Rt△BC′E中,![]() =2,
=2,
∴∠C′BE=30°,
①当点C′在BC的上方时,

如图1,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形,
∴EG=AB=6,AG=BE=8,
∵∠C′BE=30°,∠BC′E=90°,
∴∠BEC′=60°,
由折叠的性质得,∠C′EF=′CEF,
∴∠C′EF=∠CEF=60°,
∵AD∥BC
∴∠HFE=∠CEF=60°,
∴△EFH是等边三角形,
∴在Rt△EFG中,EG=6,
∴GF=2![]() ,
,
∴AF═8+2![]() ;
;
②当点C′在BC的下方时,
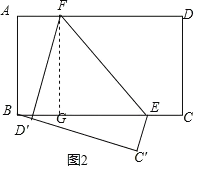
如图2,过F作FG⊥AD于G,D′F交BE于H,
同①可得,四边形ABGF是矩形,△EFH是等边三角形,
∴AF=BG,FG=AB=6,∠FEH=60°,
在Rt△EFG中,GE=2![]() ,
,
∵BE=8,
∴BG=82![]() ,
,
∴AF=82![]() ,
,
综上所述,AF的长是8+2![]() 或82
或82![]() .
.
故答案为:8+2![]() 或82
或82![]() .
.
点睛: 本题考查了翻折变换折叠问题,正确的作出图形是解题的关键.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.

解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(![]() ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BF=CE.
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
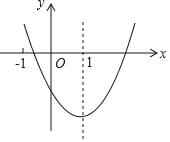
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com