
 已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则:
已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则:分析 (1)首先过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,由双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A、点B,且AE=AB=BF,可设点A的坐标为(m,$\frac{4}{m}$),得到点B的坐标为:(2m,$\frac{2}{m}$),则可由S△OAB=S△OAM+S梯形AMNB-S△OBN,求得△AOB的面积,易得△ODH∽△OBN,可得($\frac{OD}{OB}$)2=$\frac{1}{2}$,继而可得$\frac{OC}{OA}$=$\frac{OD}{OB}$,所以AB∥CD
(2)由$\frac{OC}{OA}$=$\frac{OD}{OB}$,∠COD=∠AOB则可证得△COD∽△AOB,然后由相似三角形面积比等于相似比的平方,求得答案.
解答 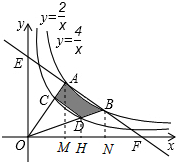 解:(1)如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,
解:(1)如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,
∴AM∥DH∥BN∥y轴,
设点A的坐标为:(m,$\frac{4}{m}$),
∵AE=AB=BF,
∴OM=MN=NF,
∴点B的坐标为:(2m,$\frac{2}{m}$),
∴S△OAB=S△OAM+S梯形AMNB-S△OBN=2+$\frac{1}{2}$×($\frac{2}{m}$+$\frac{4}{m}$)×(2m-m)-2=3,
∵DH∥BN,
∴△ODH∽△OBN,
∴$\frac{OD}{OB}$=$\frac{DH}{BN}$=$\frac{OH}{ON}$,
∵DH•OH=2,BN•ON=4,
∴($\frac{OD}{OB}$)2=$\frac{2}{4}$=$\frac{1}{2}$,
同理:($\frac{OC}{OA}$)2=$\frac{1}{2}$,
∴$\frac{OC}{OA}$=$\frac{OD}{OB}$,
∴AB∥CD
故答案为:平行;
(2)∵$\frac{OC}{OA}$=$\frac{OD}{OB}$,∠COD=∠AOB,
∴△COD∽△AOB,
∴$\frac{{S}_{△COD}}{{S}_{△AOB}}$=( $\frac{OD}{OB}$)2=$\frac{1}{2}$,
∴S△COD=$\frac{3}{2}$,
∴S四边形ABDC=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了反比例函数中k的几何意义以及相似三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意掌握方程思想与数形结合思想的应用.


科目:初中数学 来源:2017届广东省东莞市堂星晨学校九年级第一次模拟数学试卷(解析版) 题型:填空题
如图,已知正六边形ABCDEF的外接圆半径为2cm,则正六边形的边心距是__cm.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:判断题
如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.

(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:单选题
ABCD是边长为1的正方形,△BPC是等边三角形,则△BPD的面积为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:单选题
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
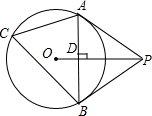 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
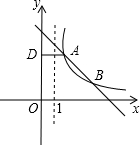 已知函数y=$\frac{m}{x-1}$(x>1,m>0)的图象C是由函数y=$\frac{m}{x}$(x>0,m>0)的图象向右平移一个单位得到,如图所示,函数y=-x+5的图象与图象C交于A,B两点,作AD⊥y轴,垂足为D.
已知函数y=$\frac{m}{x-1}$(x>1,m>0)的图象C是由函数y=$\frac{m}{x}$(x>0,m>0)的图象向右平移一个单位得到,如图所示,函数y=-x+5的图象与图象C交于A,B两点,作AD⊥y轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com