Question

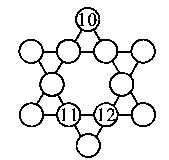
请把1～9这九个连续整数填入图中空着的圆圈里，使每一条直线上的四个数之和都相等．

Answer 1

答案：略
解析：

解：图中6条直线中的24个圆圈，其中所填的数恰好是1～12各被取了2次，因此每条直线上的4个数之和为(1＋12)×12÷6＝26．由26－(11＋12)＝3＝1＋2，得在11、12的两边分别填上1、2，由26－(10＋1)＝15＝6＋9＝7＋8与26－(10＋2)＝14＝5＋9＝6＋8．看出6、9不能同时填在10、1之间，只能填上7、8，否则10与2之间就无数可填．这时还剩下3、4、6，由26－(11＋8)＝7＝3＋4，26－(11＋7)＝8，则11的左上方是8，由26－(12＋9)＝5，26－(12＋5)＝9＝3＋6，则12的右上方是5，且这两条直线的交点为5，如图②．