
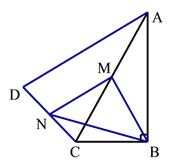
【题目】如图,在四边形ABCD中,∠ABC=90°![]() ,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分![]() ,AC=2, 写出求BN长的思路.
,AC=2, 写出求BN长的思路.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)分别根据“斜边上的中线等于斜边的一半”与中位线定理得到边之间的关系,再结合已知条件进行等量代换即可。(2))由已知可证∠DAC=∠CAB=30°,BM=AM=![]() AC=1,根据三角形外角性质可证∠CMB=60°,根据三角形中位线定理可证MN∥AD,MN=
AC=1,根据三角形外角性质可证∠CMB=60°,根据三角形中位线定理可证MN∥AD,MN=![]() AD=1, ∠DAC=∠NMC=30°可得三角形NMB是直角三角形,根据三角形勾股定理可得出BN的长
AD=1, ∠DAC=∠NMC=30°可得三角形NMB是直角三角形,根据三角形勾股定理可得出BN的长![]() .
.
试题解析:
(1)证明:∵∠ABC=90°,M为AC中点
∴BM=![]() AC
AC
∵M为AC中点,N为DC中点
∴MN=![]() AD
AD
∵AD=AC
∴BM=MN

(2)由已知可证∠DAC=∠CAB=30°,
BM=AM=![]() AC=1
AC=1
根据三角形外角性质可证∠CMB=60°
根据三角形中位线定理可证MN∥AD,MN=![]() AD=1, ∠DAC=∠NMC=30°
AD=1, ∠DAC=∠NMC=30°
可得三角形NMB是直角三角形
根据三角形勾股定理可得出BN的长![]()


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】填空题:
(1)-6的倒数是_____,-6的倒数的倒数是_______,-6的相反数是______,-6的相反数的相反数是_______;
(2)当两数_____时,它们的和为0;
(3)当两数_____时,它们的积为0;
(4)当两数_____时,它们的积为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
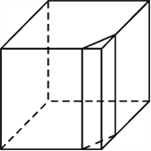
【题目】如图所示,用一个平面去截掉一个正方体的一条棱.
(1)剩下的几何体的形状是什么?
(2)剩下的几何体有几个顶点?几条棱?几个面?
(3)若按此方法截掉一个n棱柱的一条棱,则剩下的几何体有几个顶点?几条棱?几个面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若⊙O的半径为R,直线l与⊙O有公共点,若圆心到直线l的距离为d,则d与R的大小关系是( ).
A. d>R B. d<R C. d≥R D. d≤R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第22题)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:

(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
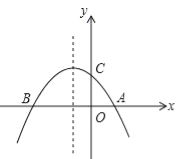
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
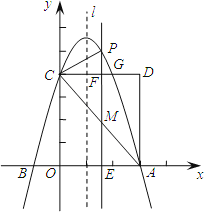
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com