
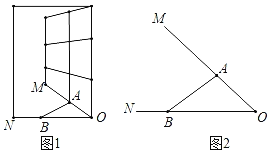
【题目】如图1,一扇窗户打开一定角度,其中一端固定在窗户边OM上的点A处,另一端B在边ON上滑动,图2为某一位置从上往下看的平面图,测得∠ABO为37°,∠AOB为45°,OB长为35厘米,求AB的长(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
科目:初中数学 来源: 题型:
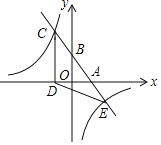
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
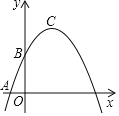
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在ABC中,小明按照下列作图步骤进行尺规作图(示意图与作图步骤如表),那么交点O是△ABC的( )
示意图 | 作图步骤 |
| (1)分别以点B、C为圆心,大于 (2)分别以点A、C为圆心,大于 (3)联结AD、BE,相交于点O |
A.外心B.内切圆的圆心C.重心D.中心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点![]() ,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
,交AB于点E,点F为AC延长线上一点,且∠BAC=2∠CDF.
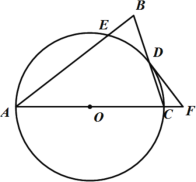
(1)求证:DF是⊙O的切线;
(2)连接DE,求证:DE=DB;
(3)若![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
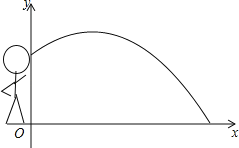
【题目】如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+![]() x+
x+![]() (a为常数,a<0).
(a为常数,a<0).
(1)解释上述函数表达式中“![]() ”的实际意义;
”的实际意义;
(2)当a=﹣![]() 时,这名运动员能把铅球推出多远?
时,这名运动员能把铅球推出多远?
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过点A(﹣3,0)和点B(3,2),与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)点P是抛物线在第一象限内一点,联结AP,如果点C关于直线AP的对称点D恰好落在x轴上,求直线AP的截距;
(3)在(2)小题的条件下,如果点E是y轴正半轴上一点,点F是直线AP上一点.当△EAO与△EAF全等时,求点E的纵坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com