
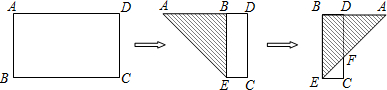
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 12 | B. | 14 | C. | 16 | D. | 36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
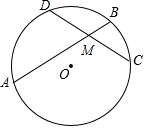 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.
已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号)
海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com