
【题目】如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.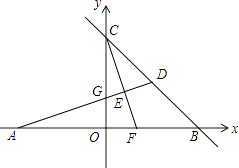
(1)求D点的坐标;
(2)求证:OF=OG;
(3)在第一象限内是否存在点P,使得△CFP为等腰直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
【答案】
(1)
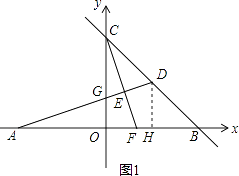
解:如图1,作DH⊥x轴于H,
∵OA=OB=OC=4,
∴AB=8,B(4,0),C(0,4),
设BC的解析式为y=kx+b,
把B,C两点代入得 ![]() ,解得:
,解得: ![]() ,
,
∴BC的解析式为y=﹣x+4,
∵△ABD的面积为8,AB=8,
∴DH=2,
所以D点的纵坐标为2,
把y=2代入y=﹣x+4得:x=2,
∴D(2,2);
(2)
解:∵CE⊥AD,
∴∠CEG=∠AOG=90°,
又∵∠AGO=∠CGE,
∴△AGO~△CGE,
∴∠GAO=∠GCE,
在△COF与△AOG中, 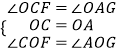 ,
,
∴△COF≌△AOG,
∴OF=OG;
(3)
解:存在,∵A(﹣4,0),D(2,2),
∴直线AD的解析式为y= ![]() x+
x+ ![]() ,
,
∴OG= ![]() ,
,
∴OF=OG= ![]() ,
,
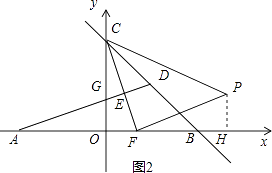
①如图2,当∠CFP=90°,FP=FC时,
过P作PH⊥x轴于H,
∴∠PHF=∠COF=90°,
∴∠OCF+∠OFC=∠OFC+∠PFH=90°,∴∠OCF=∠PFH,
在△COF与△PFH中, 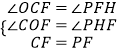 ,∴△COF≌△PFH,∴PH=OF=
,∴△COF≌△PFH,∴PH=OF= ![]() ,FH=OC=4,
,FH=OC=4,
∴OH= ![]() ,
,
∴P1( ![]() ,
, ![]() );
);
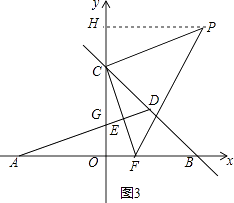
②如图3,当∠PCF=90°,CP=FC时,同理证得△PHC≌△CFO,
∴PH=OC=4,CH=OF= ![]() ,
,
∴OH= ![]() ,
,
∴P2(4, ![]() );
);
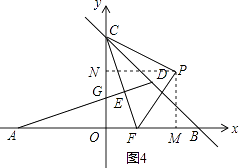
③如图4,当∠CPF=90°,PC=PF时,
过P作PM⊥x轴于M,PN⊥y轴于N,
∴四边形PNOM是矩形,
∴∠NPM=90°,
∴∠CPN+∠NPF=∠NPF+∠FPM=90°,
∴∠CPN=∠FPM,
在△CPN与△FPM中, 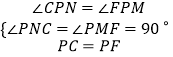 ,
,
∴△PNC≌△PMF,
∴PN=PM,CN=FM,
∴矩形PNOM是正方形,
∴ON=OM,
∴4﹣CN= ![]() +CN,
+CN,
∴CN=CM= ![]() ,
,
∴PN=PM= ![]() ,
,
∴P3( ![]() ,
, ![]() ),
),
综上所述:P的坐标为( ![]() ,
, ![]() ),(4,
),(4, ![]() ),(
),( ![]() ,
, ![]() ).
).
【解析】(1)根据已知条件得到AB=8,B(4,0),C(0,4),待定系数法求得BC的解析式为y=﹣x+4,根据三角形的面积得到DH=2,即可得到结论;(2)根据已知条件得到△AGO~△CGE,由相似三角形的性质得到∠GAO=∠GCE,根据全等三角形的性质即可得到结论;(3)根据直线AD的解析式y= ![]() x+
x+ ![]() ,求得OF=OG=
,求得OF=OG= ![]() ,①如图2,当∠CFP=90°,FP=FC时,过P作PH⊥x轴于H,根据全等三角形的性质得到PH=OF=
,①如图2,当∠CFP=90°,FP=FC时,过P作PH⊥x轴于H,根据全等三角形的性质得到PH=OF= ![]() ,FH=OC=4,于是得到P1(
,FH=OC=4,于是得到P1( ![]() ,
, ![]() );②如图3,当∠PCF=90°,CP=FC时,根据全等三角形的性质得到PH=OC=4,CH=OF=
);②如图3,当∠PCF=90°,CP=FC时,根据全等三角形的性质得到PH=OC=4,CH=OF= ![]() ,于是得到P2(4,
,于是得到P2(4, ![]() );③如图4,当∠CPF=90°,PC=PF时,根据全等三角形的性质得到PN=PM,CN=FM,根据ON=OM,列方程得到CN=CM=
);③如图4,当∠CPF=90°,PC=PF时,根据全等三角形的性质得到PN=PM,CN=FM,根据ON=OM,列方程得到CN=CM= ![]() ,于是得到P3(
,于是得到P3( ![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.![]()
(1)点C表示的数是;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是(用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
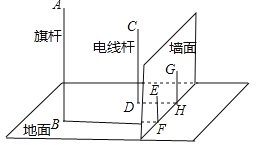
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
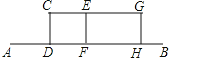
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年国家启动实施农村义务教育学生营养改善计划,截至2014年4月,我省开展营养改善试点中小学达17580所,17580这个数用科学记数法可表示为( )
A. 17.58×103B. 175.8×104C. 1.758×105D. 1.758×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com