
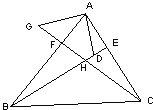
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
【答案】(1)证明见解析;(2)AD⊥AG,证明见解析.
【解析】试题分析:(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.
试题解析:(1)∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,
又∵∠BHF=∠CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
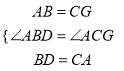 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等);
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.


科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
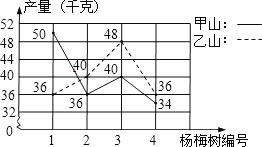
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求方程x2+bx+c=x+m的解.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.
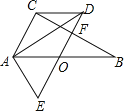
(1)求证:OD⊥BC;
(2)求证:四边形AODC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第n次操作后,剩下的长方形为正方形,则称原长方形为n阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.
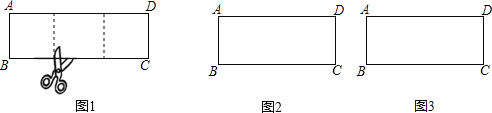
(1)判断与操作:
如图2,长方形ABCD长为10,宽为4,它是奇异长方形,请写出它是 阶奇异长方形,并在图中画出裁剪线;
(2)探究与计算:
已知长方形ABCD的一边长为30,另一边长为a (a<30),且它是3阶奇异长方形,请画出所有可能的长方形ABCD及裁剪线的示意图,并求出相应的a值.
查看答案和解析>>
科目:初中数学 来源: 题型:
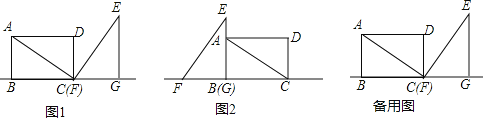
【题目】已知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).
(1)当t为何值时,点D落在线段EF上?
(2)设在平移过程中△EFG与矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出相应的t的取值范围;
(3)在平移过程中,当点G与点B重合时(如图2),将△CBA绕点B逆时针旋转得到△C1A1B,直线EF与C1A1所在直线交于P点,与C1B所在直线交于点Q.在旋转过程中,△ABC的旋转角为α(0°<α<180°),是否存在这样的α,使得△C1PQ为等腰三角形?若存在,请写出α的度数,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com