
 画图:已知线段a、b.
画图:已知线段a、b.科目:初中数学 来源: 题型:填空题
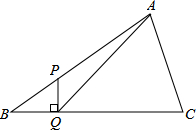 如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.
如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:
如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;
在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.14×103 | B. | 2.14×104 | C. | 21.4×102 | D. | 0.214×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com