
【题目】方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
⑴求v关于t的函数表达式;
⑵方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的交点
轴的交点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
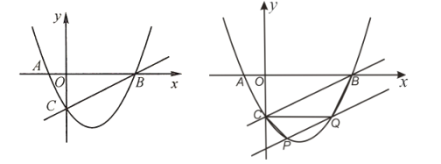
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,过点
下方抛物线上的一点,过点![]() 作
作![]() 的平行线交抛物线于点
的平行线交抛物线于点![]() (点
(点![]() 在点
在点![]() 右侧),连结
右侧),连结![]() 、
、![]() ,当
,当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 点的坐标;
点的坐标;
(3)现将该抛物线沿射线![]() 的方向进行平移,平移后的抛物线与直线
的方向进行平移,平移后的抛物线与直线![]() 的交点为
的交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的下方),与
的下方),与![]() 轴的右侧交点为
轴的右侧交点为![]() ,当
,当![]() 与
与![]() 相似,求出点
相似,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(1,0).如图,点M是直线l上的一点,点A关于点M的对称点为点B,点B关于直线l的对称点为点C.若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),则点B的坐标为_____及n的值为______.
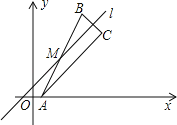
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
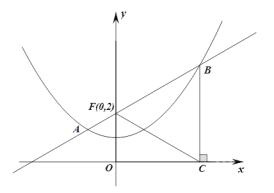
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司甲、乙两名快递员7月上旬10天里派送快递,乙比甲晚工作一段时间,工作期间快递员甲因事停工3天,各自的工作效率一定,他们各自的工作量![]() (件)随工作时间
(件)随工作时间![]() (天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
(天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
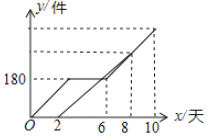
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
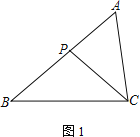

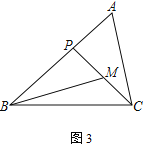
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com