
【探究发现】
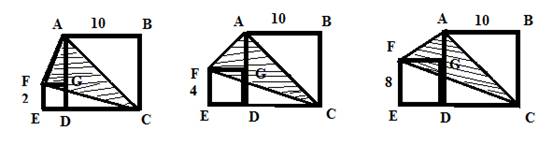
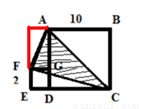
按图中方式将大小不同的两个正方形放在一起,分别求出阴影部分(⊿ACF)的面积。(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)
1.S1= cm2; S2= cm2; S3= cm2.
2.归纳总结你的发现:
【推理反思】
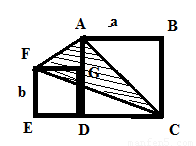
按图中方式将大小不同的两个正方形放在一起,设小正方形的边长是bcm,大正方形的边长是acm,求:阴影部分(⊿ACF)的面积。
【应用拓展】
1.按上图方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
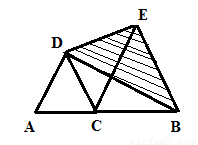
2.如图(1),C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形⊿ACD和等边三角形⊿CBE,若⊿CBE的边长是1cm,则图中阴影三角形的面积是 cm2.
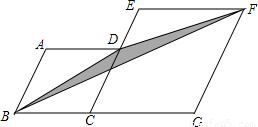
3.如图(2),菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是
(1) (2)
见解析
【解析】
试题分析:
【探索发现】如图补全图形,是一个大长方形减去三个三角形,其余两个一样.经过计算可以总结出阴影部分的面积等于大正方形的面积的一半.
【推理反思】同上
【应用拓展】(1)由探索发现的总结得阴影部分的面积等于大正方形的面积的一半.
(2)由于⊿ACD和⊿CBE是等边三角形,所以CD//BE,即△DBE和△CBE以BE为底且高相等,求出△CBE的面积就是△DBE的面积了.
(3)设BF与CE相交于点G,利用相似三角形对应边成比例列式求出CG,再求出DG的长,然后求出两个菱形的高,再根据三角形的面积公式列式计算即可得解.
试题解析:【探索发现】
解:(1)S1=12×10 
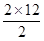
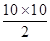 =120
8 12 50=50
=120
8 12 50=50
S2=14×10 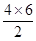

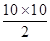 =140
12 28 50=50
=140
12 28 50=50
S3=18×10 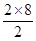
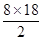
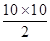 =180
8 72 50=50
=180
8 72 50=50
(2)归纳发现:阴影部分的面积等于大正方形面积的一半.
【推理反思】
解:S△AFC=a(a+b) 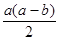
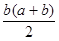
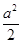 =
=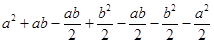 =
=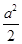
【应用拓展】解:(1)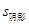 =
=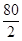 =40
=40
(2)∵⊿ACD和⊿CBE是等边三角形
∴∠ACD=∠CBE=60°
∴CD//BE
因此,△DBE和△CBE以BE为底的高相等
∴S△DBE=S△CBE=1
(3)如图,设BF与CE相交于点G,在菱形ECGF中,CE∥GF,
∴△BCG∽△BGF,
∴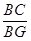 =
=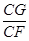 ,即
,即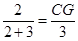 ,
,
解得CG=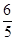 ,
,
∴DG=CD CG=2 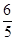 =
=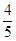
∵菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,
∴菱形ABCD的CD边上的高为 , 菱形ECGF的CE边长的高为
, 菱形ECGF的CE边长的高为 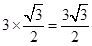
∴图中阴影部分的面积=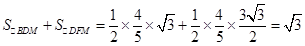
考点:1.组合图形的面积;2.菱形的性质


科目:初中数学 来源: 题型:

 ▲ ,
▲ ,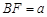 ,
,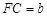 ,DE与BC间的距离为
,DE与BC间的距离为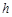 .请证明S2=4S1 S2.
.请证明S2=4S1 S2.
查看答案和解析>>
科目:初中数学 来源:2012届江苏无锡滨湖中学九年级中考二模数学试卷(带解析) 题型:解答题
在图形的全等变换中,有旋转变换,翻折(轴对称)变换和平移变换.一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.

【小题1】第一小组的同学发现,在如图1-1的矩形ABCD中,AC、BD相交于点O,Rt△ADC可以由Rt△ABC经过一种变换得到,请你写出这种变换的过程是 ▲ .
【小题2】第二小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图2-1);再沿GC折叠,使点B落在EF上的点B'处(如图2-2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
【小题3】第三小组的同学,在一个矩形纸片上按照图3-1的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图3-2.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.
【小题4】探究活动结束后,老师给大家留下了一道探究题:
如图4-1,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.
查看答案和解析>>
科目:初中数学 来源:2012届浙江省金华地区九年级下学期第一次月考数学卷 题型:解答题
问题背景
【小题1】(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空: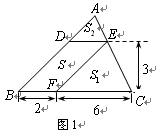
四边形DBFE的面积 ▲ ,
▲ ,
△EFC的面积S1= ▲ ,
△ADE的面积S2= ▲ .
探究发现
【小题2】(2)在(1)中,若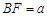 ,
, ,DE与BC间的距离为
,DE与BC间的距离为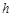 .请证明S2=4S1 S2.
.请证明S2=4S1 S2.
拓展迁移
【小题3】(3)如图2,平行四边形DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com